Jarak Dua Bidang pada Dimensi Tiga
Blog Koma - Konsep jarak terakhir yang akan kita bahas yang berkaitan jarak pada dimensi tiga tingkat SMA adalah Jarak Dua Bidang pada Dimensi Ti…
Read more »
Jarak Garis dan Bidang pada Dimensi Tiga
Blog Koma - Pada artikel ini kita akan membahas materi Jarak Garis dan Bidang pada Dimensi Tiga . Seperti yang telah kita pelajari, konsep jarak pa…
Read more »
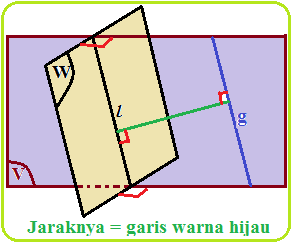
Jarak Dua Garis pada Dimensi Tiga
Blog Koma - Pada artikel ini kita akan membahas materi Jarak Dua Garis pada Dimensi Tiga . Sebelumnya juga telah kita bahas jarak pada dimensi tig…
Read more »
Aplikasi Vektor pada Bangun Ruang dan Datar
Blog Koma - Pada artikel ini kita akan membahas materi Aplikasi Vektor pada Bangun Ruang dan Datar . Dengan mengetahui " panjang vektor "…
Read more »
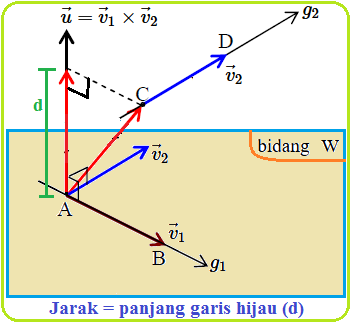
Aplikasi Vektor : Jarak Dua Garis
Blog Koma - Aplikasi vektor yang akan kita bahas pada artikel ini adalah Aplikasi Vektor : Jarak Dua Garis . Aplikasi vektor dalam bangun datar at…
Read more »
Aplikasi Vektor : Volume Bangun Ruang
Blog Koma - Pada artikel ini kita akan membahas materi Aplikasi Vektor : Volume Bangun Ruang yang merupakan salah satu bagian dari aplikasi vekto…
Read more »
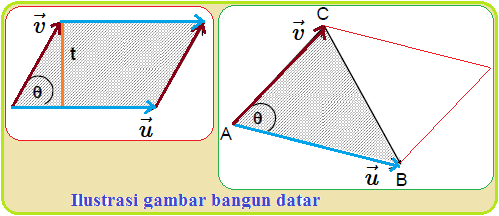
Aplikasi Vektor : Luas Bangun Datar
Blog Koma - Setelah mempelajari materi " aplikasi vektor : jarak titik ke garis ", pada artikel ini kita lanjutkan lagi pembahasan aplik…
Read more »