Jarak Dua Bidang pada Dimensi Tiga
Misalkan terdapat dua bidang U dan V yang tidak saling berpotongan (jika berpotongan maka jaraknya nol). Perhatikan gambar ilustrasi di atas,
langkah-langkah menentukan jarak kedua bidang tersebut yaitu :
1). Buat bidang W yang tegak lurus dengan bidang U dan bidang V,
2). Misalkan garis $ g $ dan $ h $ adalah perpotongan bidang W dengan bidang U dan bidang W dengan bidang V,
3). Jarak U ke V = jarak garis $ g $ ke $ h $.
Ada dua cara untuk menentukan jarak $ g $ dan $ h $ yaitu :
Cara I :
i). Pilih sembarang satu titik P pada salah satu garis,
ii). Jarak $ g $ dan $ h $ adalah jarak titik titik P ke garis yang tidak memuat P.
Cara II :
a). buat bidang T yang tegak lurus garis $ g $ dan $ h $,
b). bidang U memotong garis $ g $ dan $ h $ masing-masing di titik P dan Q,
c). Jarak $ g $ ke $ h $ = jarak titik P ke titik Q.
1). Buat bidang W yang tegak lurus dengan bidang U dan bidang V,
2). Misalkan garis $ g $ dan $ h $ adalah perpotongan bidang W dengan bidang U dan bidang W dengan bidang V,
3). Jarak U ke V = jarak garis $ g $ ke $ h $.
Ada dua cara untuk menentukan jarak $ g $ dan $ h $ yaitu :
Cara I :
i). Pilih sembarang satu titik P pada salah satu garis,
ii). Jarak $ g $ dan $ h $ adalah jarak titik titik P ke garis yang tidak memuat P.
Cara II :
a). buat bidang T yang tegak lurus garis $ g $ dan $ h $,
b). bidang U memotong garis $ g $ dan $ h $ masing-masing di titik P dan Q,
c). Jarak $ g $ ke $ h $ = jarak titik P ke titik Q.
Contoh Soal Jarak Dua Bidang pada Dimensi Tiga
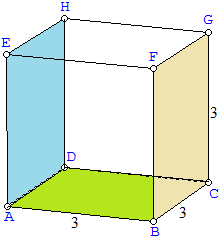
1). Sebuah kubus ABCD.EFGH memiliki panjang rusuk 3 cm. Tentukan jarak bidang BCGF dan ADHE!
Penyelesaian :
*). Buat bidang yang tegak lurus BCGF dan ADHE yaitu bidang ABFE.
*). ABFE memotong BCGF dan ADHE di BF dan AE, sehingga jaraknya adalah BF ke AE.
*). Buat bidang tegak lurus BF dan AE yaitu ABCD dimana ABCD memotong BF dan AE di A dan B, sehingga jaraknya adalah A ke B yaitu 3 cm.
Jadi, jarak bidang BCGF dan ADHE adalah 3 cm.
2). Sebuah kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Tentukan jarak bidang BDE dan CFH!
Penyelesaian :
*). Buat bidang yang tegak lurus BDE dan CFH yaitu bidang ACGE.
*). ACGE memotong BDE dan CFH di PE dan CQ, sehingga jaraknya adalah PE ke CQ.
*). Kita pilih titik P pada PE, sehingga jaraknya adalah P ke CQ yaitu panjang PN. Untuk memudahkan perhitungan PN, kita fokus pada segitiga CPQ yang siku-siku di P.
*). Menentukan panjang sisi-sisi CPQ
$ CP = \frac{1}{2}AC = 3\sqrt{2} \, $ cm
PQ = CG = 6 cm
$ CQ = \sqrt{CP^2 + PQ^2} = \sqrt{(3\sqrt{2})^2 + 6^2} = 3\sqrt{6}= 3\sqrt{2} \sqrt{3} $
*). Konsep luas segitiga CPQ :
$ \begin{align} \frac{1}{2}.CP.PQ & = \frac{1}{2}.CQ.PN \\ CP.PQ & = CQ.PN \\ 3\sqrt{2} . 6 & = 3\sqrt{2} \sqrt{3} .PN \\ 6 & = \sqrt{3} .PN \\ PN & = \frac{6}{\sqrt{3}} = 2\sqrt{3} \end{align} $
Jadi, jarak BDE dan CFH adalah $ 2\sqrt{3} \, $ cm.
3). Sebuah kubus ABCD.EFGH memiliki panjang rusuk 4 cm. Titik-titik P, Q, R, dan S terletak di tengah-tengah AB, EF, EH, dan AD. Titik-titik T, U, V, dan W terletak di tengah-tengah BC, FG, GH, dan CD. Tentukan jarak bidang PQRS dan TUVW!
Penyelesaian :
*). Buat bidang yang tegak lurus PQRS dan TUVW yaitu bidang ACGE.
*). ACGE memotong PQRS dan TUVW di MN dan XY, sehingga jaraknya adalah MN ke XY.
*). Buat bidang tegak lurus MN dan XY yaitu ABCD dimana ABCD memotong MN dan XY di M dan X, sehingga jaraknya adalah M ke X.
$ MX = \frac{2}{4}AC = \frac{2}{4} . 4\sqrt{2} = 2\sqrt{2} $
Jadi, jarak bidang PQRS dan TUVW adalah $ 2\sqrt{2} \, $ cm.
4). Sebuah kubus ABCD.EFGH memiliki panjang rusuk 2 cm. Titik P dan Q masing-masing terletak ditengah-tengah AE dan CG. Tentukan jarak bidang PFH dan QBD!
Penyelesaian :
*). Buat bidang yang tegak lurus PFH dan QBD yaitu bidang ACGE.
*). ACGE memotong PFH dan QBD di PX dan QY, sehingga jaraknya adalah PX ke QY.
*). Kita pilih titik X pada PX, sehingga jaraknya adalah X ke QY yaitu panjang XN. Untuk memudahkan perhitungan XN, kita fokus pada segitiga XQY.
*). Menentukan panjang sisi-sisi XQY
XY = CG = 2 cm
Pada segitiga CQY :
$ QY = \sqrt{YC^2 + CQ^2} = \sqrt{(\sqrt{2})^2 + 1^2} = \sqrt{3} \, $ cm
QX = QY = $ \, \sqrt{3} \, $ cm
Misalkan $ YN = s $, maka $ NQ = \sqrt{3} - s $
*). Menentukan $ s $ pada $ \Delta XQY $ :
$ \begin{align} t^2 \, (\Delta YNX) & = t^2 \, (\Delta QNX) \\ XY^2 - YN^2 & = XQ^2 - NQ^2 \\ 2^2 - s^2 & = (\sqrt{3})^2 - ( \sqrt{3} - s)^2 \\ 4 - s^2 & = 3 - ( 3 - 2\sqrt{3}s + s^2) \\ 4 - s^2 & = 3 - 3 + 2\sqrt{3}s - s^2 \\ 4 & = 2\sqrt{3}s \\ s & = \frac{4}{2\sqrt{3}} = \frac{2}{3}\sqrt{3} \end{align} $
*). Menentukan $ XN = t $ pada segitiga YNX :
$ \begin{align} t & = \sqrt{XY^2 - YN^2} \\ & = \sqrt{2^2 - s^2} \\ & = \sqrt{2^2 - (\frac{2}{3}\sqrt{3} )^2} \\ & = \sqrt{2^2 - \frac{4}{3}} = \frac{2}{3}\sqrt{6} \end{align} $
Jadi, jarak PFH dan QBD adalah $ \frac{2}{3}\sqrt{6} \, $ cm.
5). Sebuah limas T.ABCD dimana semua panjang rusuknya sama yaitu 8 cm. Titik P, Q, R, dan S masing-masing terletak ditengah-tengah AB, CD, TD, dan TA. Tentukan jarak PQRS dan TBC!
Penyelesaian :
*). Buat bidang yang tegak lurus PQRS dan TBC yaitu bidang TUV.
*). TUV memotong PQRS dan TBC di OK dan TV, sehingga jaraknya adalah OK ke TV.
*). Kita pilih titik O pada OK, sehingga jaraknya adalah O ke TV yaitu panjang ON. Untuk memudahkan perhitungan ON, kita fokus pada segitiga TOV.
*). Menentukan panjang sisi-sisi TOV :
$ OV = \frac{1}{2}AB = 4 \, $ cm
Pada segitiga TOB :
$ TO = \sqrt{TB^2 - OB^2} = \sqrt{8^2 - (4\sqrt{2})^2} = 4\sqrt{2} \, $ cm
Pada segitiga TVC :
$ TV = \sqrt{TC^2 - CV^2} = \sqrt{8^2 - 4^2} = 4\sqrt{3} \, $ cm
*). Konsep luas segitiga TOV :
$ \begin{align} \frac{1}{2}.TO.OV & = \frac{1}{2}.TV.ON \\ TO.OV & = TV.ON \\ 4\sqrt{2} . 4 & = 4\sqrt{3}.ON \\ ON & = \frac{4\sqrt{2}}{\sqrt{3}} = \frac{4}{3}\sqrt{6} \end{align} $
Jadi, jarak PQRS dan TBC adalah $ \frac{4}{3}\sqrt{6} \, $ cm.
6). Pada Kubus ABCD.EFGH yang memiliki panjang rusuk 4 cm. Terdapat titik P dan Q masing-masing di tengah-tengah EF dan EH. Tentukan jarak APQ dan BCGF!
Penyelesaian :
*). Perhatikan gambar contoh 6 di atas, bidang APQ dan BCGF tidak sejajar sehingga jika kedua bidang diperluas maka akan berpotongan. Disini kita akan mencari jarak terdekat antara segmen bidang APQ dan BCGF yang tampak pada kubus ABCD.EFGH tanpa adanya perluasan. Jarak terdekat akan kita peroleh dari titik P ke garis FB yaitu jarak antara P ke F sebesar 2 cm.
Jadi, jarak APQ dan BCGF adalah 2 cm.
Demikian pembahasan materi Jarak Dua Bidang pada Dimensi Tiga dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan dimensi tiga yaitu "Sudut antara Dua Garis pada Dimensi Tiga".