Nomor 1. Soal SBMPTN Mat IPA 2014 Kode 554
Nomor 11. Soal SPMB Mat IPA 2005
Nomor 21. Soal UTUL UGM Mat IPA 2015
Nomor 31. Soal SBMPTN Mat IPA 2016 Kode 251
Nomor 37. Soal UM Undip 2016 Mat dasar IPA
Update bulan Desember 2018 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya.
Nomor 45. Soal SBMPTN 2018 Matipa Kode 452
Demikian Kumpulan Soal Lingkaran Seleksi Masuk PTN lengkap dengan pembahasannya. Semoga artikel ini bermanfaat untuk kita semua.
Kumpulan Soal Lingkaran Seleksi Masuk PTN ini akan terus kami update untuk soal-soal tahun lainnya. Jika ada kritik dan saran, langsung saja ketikkan
komentar pada kolom kontar di bagian bawah setiap artikel. Silahkan juga pelajari kumpulan soal lain pada "Kumpulan Soal Matematika Per Bab Seleksi Masuk PTN". Terima Kasih.
Misalkan diberikan titik A(1, 0) dan B(0, 1) . Jika P bersifat $|\vec{PA}|:|\vec{PB}|=\sqrt{m}:\sqrt{n}$ , maka P terletak pada
lingkaran dengan persamaan ...
Nomor 2. Soal SBMPTN Mat IPA 2014 Kode 514
Jika lingkaran $x^2+y^2-2ax+b=0$ mempunyai jari-jari 2 dan menyinggung $x-y=0$ , maka nilai $a^2+b$ adalah ...
Nomor 3. Soal UTUL UGM Mat IPA 2014
Jika garis $y=mx+k$ menyinggung lingkaran $x^2+y^2-10x+6y+24=0$ di titik (8,-4) , maka nilai $m+k$ adalah ...
Nomor 4. Soal SBMPTN Mat IPA 2013 Kode 436
Persamaan lingkaran dengan pusat (-1,1) dan menyinggung garis $3x-4y+12=0 \, $ adalah ...
Nomor 5. Soal SNMPTN Mat IPA 2012 Kode 634
Lingkaran $(x-3)^2+(y-4)^2=25 $ memotong sumbu X di titik $A$ dan $B$ . Jika $P$ adalah titik pusat lingkaran tersebut,
maka $\cos \angle APB = ... $
Nomor 6. Soal SNMPTN Mat IPA 2012 Kode 634
Lingkaran $(x-4)^2 + (y-2)^2 = 64 $ menyinggung garis $x=-4 $ di titik ...
Nomor 7. Soal SNMPTN Mat IPA 2011 Kode 574
Diberikan lingkaran dengan persamaan $(x+5)^2+(y-12)^2= 14^2 $ . Jarak minimal titik pada lingkaran tersebut ke titik
asal adalah ...
Nomor 8. Soal SNMPTN Mat IPA 2009 Kode 276
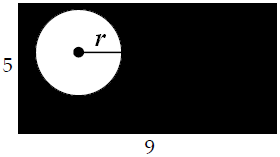
Segiempat berikut berupa persegipanjang dengan panjang sisi 5 dan 9 satuan. Luas daerah yang diarsir pada gambar berikut
4 kali luas daerah lingkaran. Jari-jari lingkaran adalah ....
Nomor 9. Soal SPMB Mat IPA 2006 
Jika lingkaran $ x^2 + y^2 + ax + by + c = 0 $ berpusat di (1, -1) menyinggung garis $ y = x $ , maka nilai $ a+b+c $ adalah ....
Nomor 10. Soal Selma UM Mat IPA 2014
Satu dari dua persamaan garis singgung dari lingkaran $ x^2 + y^2 - 2x - 4y = 0 \, $ yang tegak lurus terhadap garis
$ x - 2y + 4 = 0 \, $ adalah ....
Nomor 11. Soal SPMB Mat IPA 2005
Jika lingkaran $ x^2 + y^2 + 6x + 6y + c = 0 \, $ menyinggung garis $ x = 2, \, $
maka nilai $ c $ adalah .....
Nomor 12. Soal SPMB Mat IPA 2004
Persamaan lingkaran dengan titik pusat berada pada parabola $ y = x^2 \, $ dan menyinggung sumbu X adalah .....
Nomor 13. Soal SPMB Mat IPA 2002
Lingkaran yang sepusat dengan lingkaran $ x^2 + y^2 - 4x + 6y - 17 = 0 \, $ dan menyinggung garis $ 3x-4y + 7 = 0 \, $
mempunyai persamaan .....
Nomor 14. Soal UMPTN Mat IPA 2001
Garis $ g $ menghubungkan titik A(5,0) dan titik B($10 \cos \theta, 10 \sin \theta $). Titik P terletak pada AB sehingga AP:PB = 2:3.
Jika $ \theta \, $ berubah dai $ 0 \, $ sampai $ 2\pi $, maka titik P bergerak menelusuri kurva yang berupa .....
Nomor 15. Soal UMPTN Mat IPA 2000
Luas sebuah lingkaran adalah fungsi dari kelilingnya. Jika keliling sebuah lingkaran adalah $ x $ , maka laju perubahan
luas lingkaran terhadap kelilingnya adalah ....
Nomor 16. Soal SNMPTN Mat IPA 2014 Kode 523
Persamaan garis lurus yang melalui titik potong lingkaran-lingkaran yang melalui titik (-2,-1) dan menyinggung sumbu X dan sumbu Y adalah ....
Nomor 17. Soal SNMPTN Mat IPA 2014 Kode 542
Misalkan $ l_1 \, $ dan $ l_2 \, $ menyatakan garis yang menyinggung lingkaran $ x^2 + y^2 = r^2 \, $ berturut-turut di
$ P_1(x_1,y_1) \, $ dan $ P_2(x_2,y_2) \, $ . Jika $ l_1 \, $ dan $ l_2 \, $ berpotongan di $ (2,-1) \, $ dan titik $ (4,-1) \, $
berada pada garis yang melalui $ P_1 \, $ dan $ P_2 \, $ , maka $ r = ..... $
Nomor 18. Soal SPMK UB Mat IPA 2010
Persamaan garis singgung lingkaran dengan $ L : \, x^2 + y^2 -6x+8y=0 \, $ yang tegak lurus pada garis $ x + y = 1 \, $ adalah ....
Nomor 19. Soal UTUL UGM Mat IPA 2013
Titik pusat lingkaran yang menyinggung garis $ y = 2 \, $ di (3,2) dan menyinggung garis $ y = -x\sqrt{3} + 2 \, $ adalah ....
Nomor 20. Soal SBMPTN Mat IPA 2015 Kode 517
Misalkan titik A dan B pada lingkaran $ x^2 + y^2 - 6x - 2y + k = 0 \, $ sehingga garis singgung lingkaran di titik A dan B
berpotongan di titik C(8,1). Jika luas segiempat yang melalui A, B, C, dan pusat lingkaran adalah 12, maka $ k = .... $
Nomor 21. Soal UTUL UGM Mat IPA 2015
Jika garis $ 2x + y + 4 = 0 \, $ dan $ 2x + y -6 = 0 \, $ menyinggung lingkaran dengan pusat $(1,p) \, $ , maka persamaan lingkaran
tersebut adalah ....
Nomor 22. Soal UTUL UGM Mat IPA 2015
Persamaan lingkaran yang pusatnya terletak pada sumbu X dan melalui titik-titik potong parabola $ y = -x^2+6x \, $ dan garis
$ 2x - y = 0 \, $ adalah ....
Nomor 23. Soal UTUL UGM Mat IPA 2015 Kode 581
Diketahui titik $(1,p)$ berada pada lingkaran $ x^2 + y^2 - 2y = 0 $. Persamaan lingkaran dengan pusat $(1,p)$
dan menyinggung garis $ px+y= 4 \, $ adalah ....
A). $ x^2 + y^2 -2x - 2y - 2 = 0 \, $
B). $ x^2 + y^2 -2x - 2y - 1 = 0 \, $
C). $ x^2 + y^2 -2x - 2y = 0 \, $
D). $ x^2 + y^2 -2x + 2y - 2 = 0 \, $
E). $ x^2 + y^2 -2x + 2y - 1 = 0 $
Nomor 24. Soal UTUL UGM Mat IPA 2015 Kode 381 A). $ x^2 + y^2 -2x - 2y - 2 = 0 \, $
B). $ x^2 + y^2 -2x - 2y - 1 = 0 \, $
C). $ x^2 + y^2 -2x - 2y = 0 \, $
D). $ x^2 + y^2 -2x + 2y - 2 = 0 \, $
E). $ x^2 + y^2 -2x + 2y - 1 = 0 $
Persamaan lingkaran yang berpusat di titik $(-1,2)$ dan menyinggung
garis $ 2y+3x-14 = 0 \, $ adalah ....
A). $ (x-1)^2 + (y+2)^2 = 10 \, $
B). $ (x+1)^2 + (y-2)^2 = 10 \, $
C). $ (x-1)^2 + (y+2)^2 = 13 \, $
D). $ (x+1)^2 + (y-2)^2 = 13 \, $
E). $ (x+1)^2 + (y+2)^2 = 13 $
Nomor 25. Soal SNMPTN Mat IPA 2016 Kode 245 A). $ (x-1)^2 + (y+2)^2 = 10 \, $
B). $ (x+1)^2 + (y-2)^2 = 10 \, $
C). $ (x-1)^2 + (y+2)^2 = 13 \, $
D). $ (x+1)^2 + (y-2)^2 = 13 \, $
E). $ (x+1)^2 + (y+2)^2 = 13 $
Diketahui persegi dengan panjang sisi 12, dan setengah lingkaran dengan diameter pada
alas, seperti pada gambar. Garis CE menyinggung lingkaran
di titik F. Panjang CE = ....
A). $ 9\sqrt{2} \, $ B). $ 13 \, $ C). $ 15 \, $ D). $ 9\sqrt{3} \, $ E). $ 16 $
Nomor 26. Soal SNMPTN Mat IPA 2016 Kode 245 A). $ 9\sqrt{2} \, $ B). $ 13 \, $ C). $ 15 \, $ D). $ 9\sqrt{3} \, $ E). $ 16 $
Misalkan $ g $ adalah garis singgung lingkaran $ x^2+y^2=25 $ di titik A(3,4). Jika
garis singgung tersebut ditransformasikan dengan matriks rotasi
$ \left( \begin{matrix} \frac{3}{5} & \frac{4}{5} \\ -\frac{4}{5} & \frac{3}{5} \end{matrix} \right)$,
maka absis dari titik potong antara garis singgung lingkaran dengan
garis hasil transformasi adalah ....
A). $ \frac{7}{2} \, $ B). $ \frac{18}{5} \, $ C). $ 4 \, $ D). $ \frac{24}{5} \, $ E). $ 5 $
Nomor 27. Soal SBMPTN Mat IPA 2016 Kode 246 A). $ \frac{7}{2} \, $ B). $ \frac{18}{5} \, $ C). $ 4 \, $ D). $ \frac{24}{5} \, $ E). $ 5 $
Diketahui lingkaran menyinggung sisi-sisi persegi panjang dengan ukuran
$ 12 \times 15$, seperti pada gambar. Garis CE menyinggung lingkaran.
Panjang DE = ....
A). $ 4 \, $ B). $ 3\sqrt{2} \, $ C). $ 5 \, $ D). $ 4\sqrt{3} \, $ E). $ 6 $
Nomor 28. Soal SBMPTN Mat IPA 2016 Kode 247 A). $ 4 \, $ B). $ 3\sqrt{2} \, $ C). $ 5 \, $ D). $ 4\sqrt{3} \, $ E). $ 6 $
Misalkan $ L_1 $ lingkaran yang mempunyai radius 6 dan pusat di (0,0) dan $ L_2 $ lingkaran yang mempunyai radius 3 dan pusat
di sumbu-X positif. Jika persamaan garis singgung dalam kedua lingkaran adalah $ 4y - 3x + 30 = 0 $ , maka persamaan $ L_2 $ adalah ....
A). $ ( x - 13)^2 + y^2 = 9 \, $
B). $ ( x - 15)^2 + y^2 = 9 \, $
C). $ ( x - 16)^2 + y^2 = 9 \, $
D). $ ( x - 17)^2 + y^2 = 9 \, $
E). $ ( x - 19)^2 + y^2 = 9 \, $
Nomor 29. Soal SBMPTN Mat IPA 2016 Kode 248 A). $ ( x - 13)^2 + y^2 = 9 \, $
B). $ ( x - 15)^2 + y^2 = 9 \, $
C). $ ( x - 16)^2 + y^2 = 9 \, $
D). $ ( x - 17)^2 + y^2 = 9 \, $
E). $ ( x - 19)^2 + y^2 = 9 \, $
Diketahui $L_1 $ dan $ L_2 $ berpusat pada sumbu X dengan radius $ R_1 = 2 $ dan $ R_2 = 4 $. Suatu garis singgung dalam
dari kedua lingkaran tersebut menyinggung $ L_1 $ di F dan menyinggung $ L_2 $ di G. Garis singgung tersebut memotong sumbu X
di Q sehingga luas segitiga AFQ adalah 5 satuan luas dengan A sebagai titik pusat $ L_1 $. Jika garis singgung dalam tersebut
mempunyai gradien positif, maka besar gradiennya adalah .....
A). $ \frac{2}{3} \, $ B). $ \frac{1}{2} \, $ C). $ \frac{2}{5} \, $ D). $ \frac{1}{3} \, $ E). $ -\frac{1}{3} $
Nomor 30. Soal SBMPTN Mat IPA 2016 Kode 250 A). $ \frac{2}{3} \, $ B). $ \frac{1}{2} \, $ C). $ \frac{2}{5} \, $ D). $ \frac{1}{3} \, $ E). $ -\frac{1}{3} $
Diketahui persegi panjang dan stengah lingkaran dengan diameter pada alas,
seperti pada gambar. Garis DE menyinggung lingkaran, panjang $ CD = 6 $
dan $ CE = 8 $. Panjang $ AD = ... $
A). $ 6\sqrt{2} \, $ B). $ 9 \, $ C). $ 10 \, $ D). $ 6\sqrt{3} \, $ E). $ 9\sqrt{2} $
A). $ 6\sqrt{2} \, $ B). $ 9 \, $ C). $ 10 \, $ D). $ 6\sqrt{3} \, $ E). $ 9\sqrt{2} $
Nomor 31. Soal SBMPTN Mat IPA 2016 Kode 251
Lingkaran $L_1 $ mempunyai jari-jari 5 dengan titik pusat (0,0), sedangkan lingkaran $L_2 $ mempunyai jari-jari 3 dengan
titik pusat pada sumbu-x positif. Jika persamaan garis singgung persekutuan dalam kedua lingkaran ini adalah
$ 4x + 3y - 25 = 0 $, maka jarak titik pusat kedua lingkaran adalah ....
A). $ 8 \, $ B). $ 10 \, $ C). $ 11 \, $ D). $ 12 \, $ E). $ 14 $
Nomor 32. Soal SBMPTN Mat IPA 2016 Kode 252 A). $ 8 \, $ B). $ 10 \, $ C). $ 11 \, $ D). $ 12 \, $ E). $ 14 $
Titik $(0,b)$ adalah titik potong garis singgung persekutuan luar lingkaran $ x^2 + y^2 = 16 $ dan
$ (x-8)^2 + (y-8)^2 = 16 \, $ dengan sumbu-$y$. Nilai $ b $ adalah .....
A). $ 4\sqrt{2} \, $ B). $ 3\sqrt{2} \, $ C). $ 2\sqrt{2} \, $ D). $ 2\sqrt{3} \, $ E). $ \sqrt{3} $
Nomor 33. Soal UTUL UGM Mat IPA 2010 A). $ 4\sqrt{2} \, $ B). $ 3\sqrt{2} \, $ C). $ 2\sqrt{2} \, $ D). $ 2\sqrt{3} \, $ E). $ \sqrt{3} $
Syarat agar garis $ ax + y = 0 $ menyinggung lingkaran dengan pusat $(-1,3)$ dan jari-jari 1 adalah $ a = .... $
A). $ \frac{3}{2} \, $ B). $ \frac{4}{3} \, $ C). $ \frac{3}{4} \, $ D). $ \frac{2}{3} \, $ E). $ \frac{1}{4} $
Nomor 34. Soal SBMPTN Mat IPA 2017 Kode 165 A). $ \frac{3}{2} \, $ B). $ \frac{4}{3} \, $ C). $ \frac{3}{4} \, $ D). $ \frac{2}{3} \, $ E). $ \frac{1}{4} $
Diketahui suatu lingkaran kecil dengan radius $ 3\sqrt{2} $ melaui pusat suatu lingkaran besar yang mempunyai radius 6. Ruas garis yang
menghubungkan dua titik potong lingkaran merupakan diameter dari lingkaran kecil, seperti pada gambar. Luas daerah irisan kedua
lingkaran adalah ....
A). $ 18\pi + 18 \, $ B). $ 18\pi - 18 \, $
C). $ 14\pi + 14 \, $ D). $ 14\pi - 15 \, $
E). $ 10\pi + 10 $
Nomor 35. Soal UTUL UGM Mat IPA 2017 Kode 713 A). $ 18\pi + 18 \, $ B). $ 18\pi - 18 \, $
C). $ 14\pi + 14 \, $ D). $ 14\pi - 15 \, $
E). $ 10\pi + 10 $
Titik pusat lingkaran L terletak di kuadran I dan terletak pada garis $ y = 2x + 1 $. Jika
lingkaran L menyinggung sumbu Y di titik ($0,11$), maka persamaan lingakran L adalah ....
A). $ x^2 + y^2 - 5x - 11y = 0 \, $
B). $ x^2 + y^2 + 5x + 11y - 242 = 0 \, $
C). $ x^2 + y^2 - 10x - 22y + 121 = 0 \, $
D). $ x^2 + y^2 - 5x + 11y = 0 \, $
E). $ x^2 + y^2 + 10x + 22y - 363 = 0 \, $
Nomor 36. Soal UTUL UGM Mat IPA 2017 Kode 814 A). $ x^2 + y^2 - 5x - 11y = 0 \, $
B). $ x^2 + y^2 + 5x + 11y - 242 = 0 \, $
C). $ x^2 + y^2 - 10x - 22y + 121 = 0 \, $
D). $ x^2 + y^2 - 5x + 11y = 0 \, $
E). $ x^2 + y^2 + 10x + 22y - 363 = 0 \, $
Persamaan lingkaran yang melalui perpotongan dua lingkaran
$ L_1 \equiv x^2+y^2 - 2x - 2y - 2 = 0 $ dan $ L_2 \equiv x^2+y^2 + 2x - 6y +6 = 0 $
serta berpusat di garis $ g \equiv x - 2y = 5 $ adalah ....
A). $ x^2 + y^2 - 6x + 2y - 5 = 0 \, $
B). $ x^2 + y^2 - 6x + 2y - 10 = 0 \, $
C). $ x^2 + y^2 + 6x + 8y - 5 = 0 \, $
D). $ x^2 + y^2 + 6x + 8y - 10 = 0 \, $
E). $ x^2 + y^2 + 6x + 8y = 0 \, $
Update bulan November 2017 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya. A). $ x^2 + y^2 - 6x + 2y - 5 = 0 \, $
B). $ x^2 + y^2 - 6x + 2y - 10 = 0 \, $
C). $ x^2 + y^2 + 6x + 8y - 5 = 0 \, $
D). $ x^2 + y^2 + 6x + 8y - 10 = 0 \, $
E). $ x^2 + y^2 + 6x + 8y = 0 \, $
Nomor 37. Soal UM Undip 2016 Mat dasar IPA
Diberikan dua buah lingkaran :
$ L_1 \equiv x^2 + y^2 - 2x - 2y + 1 = 0 $ dan $ L_2 \equiv x^2 + y^2 - 2x + 4y + 1 = 0 $
Kedudukan lingkaran $ L_1 $ dan lingkaran $ L_2 $ yang paling tepat adalah ....
A). Tidak berpotongan
B). Berpotongan di dua titik
C). Bersinggungan luar
D). Bersinggungan dalam
E). $ L_1 $ berada di dalam $ L_2 $
Nomor 38. Soal UM Undip 2016 Mat dasar IPA $ L_1 \equiv x^2 + y^2 - 2x - 2y + 1 = 0 $ dan $ L_2 \equiv x^2 + y^2 - 2x + 4y + 1 = 0 $
Kedudukan lingkaran $ L_1 $ dan lingkaran $ L_2 $ yang paling tepat adalah ....
A). Tidak berpotongan
B). Berpotongan di dua titik
C). Bersinggungan luar
D). Bersinggungan dalam
E). $ L_1 $ berada di dalam $ L_2 $
Diketahui lingkaran $ x^2 + y^2 - 6x + 8y = 0 $ memotong sumbu-$y$ di titik A dan B. Jika P
adalah titik pusat lingkaran tersebut, maka nilai $ \cos \angle APB = .... $
A). $ -\frac{14}{25} \, $ B). $ -\frac{7}{25} \, $ C). $ \frac{7}{25} \, $ D). $ \frac{12}{25} \, $ E). $ \frac{14}{25} \, $
Nomor 39. Soal UM UGM 2009 Mat IPA A). $ -\frac{14}{25} \, $ B). $ -\frac{7}{25} \, $ C). $ \frac{7}{25} \, $ D). $ \frac{12}{25} \, $ E). $ \frac{14}{25} \, $
Lingkaran dengan titik pusat $(a,b)$ menyinggung sumbu $ x $ dan garis $ y = x $
jika jari-jari $ |b|$ dan
A). $ a - (\sqrt{2} +1) b = 0 \, $
B). $ a - (\sqrt{2} -1) b = 0 \, $
C). $ (\sqrt{2} +1) a - b = 0 \, $
D). $ (\sqrt{2} -1)a - b = 0 \, $
E). $ a - \sqrt{2} b = 0 \, $
Nomor 40. Soal UM UGM 2005 Mat IPA A). $ a - (\sqrt{2} +1) b = 0 \, $
B). $ a - (\sqrt{2} -1) b = 0 \, $
C). $ (\sqrt{2} +1) a - b = 0 \, $
D). $ (\sqrt{2} -1)a - b = 0 \, $
E). $ a - \sqrt{2} b = 0 \, $
Lingkaran dengan titik pusat $ (0,1) $ dan jari-jari 2 memotong hiperbola
$ x^2 - 2y^2 + 3y - 1 = 0 $ di titik $ (x_1,y_1) $ dan $ (x_2,y_2) $.
Nilai $ 4\left( \frac{1}{y_1^2} + \frac{1}{y_2^2} \right) = .... $
A). $ 34 \, $ B). $ 35 \, $ C). $ 36 \, $ D). $ 37 \, $ E). $ 38 $
Nomor 41. Soal UM UGM 2004 Mat IPA A). $ 34 \, $ B). $ 35 \, $ C). $ 36 \, $ D). $ 37 \, $ E). $ 38 $
Diketahui sebuah lingkaran L : $ x^2 + y^2 + y - 24 = 0 $. Jika melalui titik P(1,6)
dibuat garis singgung pada L, maka jarak dari P ke titik singgung tadi adalah ....
A). $ 1 \, $ B). $ 2 \, $ C). $ 3 \, $ D). $ 4 \, $ E). $ 5 $
Nomor 42. Soal UM UGM 2003 Mat IPA A). $ 1 \, $ B). $ 2 \, $ C). $ 3 \, $ D). $ 4 \, $ E). $ 5 $
Lingkaran $ x^2 + y^2 - 6x - 6y + 6 = 0 $ mempunyai kekhususan sebagai berikut ....
A). menyinggung $ y = 0 $
B). menyinggung $ x = 0 $
C). berpusat di O(0,0)
D). titik pusatnya terletak pada $ x - y = 0 $
E). berjari-jari 3
Nomor 43. Soal UM UNDIP 2017 Mat IPA A). menyinggung $ y = 0 $
B). menyinggung $ x = 0 $
C). berpusat di O(0,0)
D). titik pusatnya terletak pada $ x - y = 0 $
E). berjari-jari 3
Persamaan lingkaran melalui titik $ A(-1,2) $ dan $ B(3,8) $ adalah ....
A). $ x^2 + y^2 - 2x + 10y + 13 = 0 \, $
B). $ x^2 + y^2 - 2x - 10y + 13 = 0 \, $
C). $ x^2 + y^2 + 2x - 10y - 13 = 0 \, $
D). $ x^2 + y^2 - 10x -2y + 13 = 0 \, $
E). $ x^2 + y^2 - 2x + 10y 13 = 0 \, $
Nomor 44. Soal UM UNDIP 2017 Mat IPA A). $ x^2 + y^2 - 2x + 10y + 13 = 0 \, $
B). $ x^2 + y^2 - 2x - 10y + 13 = 0 \, $
C). $ x^2 + y^2 + 2x - 10y - 13 = 0 \, $
D). $ x^2 + y^2 - 10x -2y + 13 = 0 \, $
E). $ x^2 + y^2 - 2x + 10y 13 = 0 \, $
Salah satu persamaan garis singgung pada lingkaran $ x^2 + y^2 + 2x - 19 = 0 $ yang dapat
di tarik dari titik $ T(1,6) $ adalah ....
A). $ x - 2y + 11 = 0 \, $
B). $ x + 2y - 11 = 0 \, $
C). $ 2x - y + 8 = 0 \, $
D). $ -2x + y - 8 = 0 \, $
E). $ 2x + y - 11 = 0 $
A). $ x - 2y + 11 = 0 \, $
B). $ x + 2y - 11 = 0 \, $
C). $ 2x - y + 8 = 0 \, $
D). $ -2x + y - 8 = 0 \, $
E). $ 2x + y - 11 = 0 $
Update bulan Desember 2018 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya.
Nomor 45. Soal SBMPTN 2018 Matipa Kode 452
Jika lingkaran $ x^2 + y^2 -ax - ay + a = 0 $ mempunyai panjang jari-jari $ \frac{1}{2}a $,
maka nilai $ a $ adalah .....
A). $ 1 \, $ B). $ 2 \, $ C). $ 3 \, $ D). $ 4 \, $ E). $ 5 $
Nomor 46. Soal SBMPTN 2018 Matipa Kode 452 A). $ 1 \, $ B). $ 2 \, $ C). $ 3 \, $ D). $ 4 \, $ E). $ 5 $
Diketahui dua lingkaran $ x^2+y^2 = 2 $ dan $ x^2+y^2=4 $. Garis $ l_1 $ menyinggung
lingkaran pertama di titik $ (1,-1) $. Garis $ l_2 $ menyinggung lingkaran kedua dan
tegak lurus dengan garis $ l_1 $. Titik potong garis $ l_1 $ dan $ l_2 $ adalah .....
A). $ ( 1+\sqrt{2} , \sqrt{2} - 1) \, $ B). $ ( 1-\sqrt{2} , \sqrt{2} - 1) \, $
C). $ ( 1+\sqrt{2} , \sqrt{2} + 1) \, $ D). $ ( 1-\sqrt{2} , \sqrt{2} - 2) \, $
E). $ ( 1+\sqrt{2} , \sqrt{2} + 2) $
Nomor 47. Soal UM UNDIP 2018 Matipa A). $ ( 1+\sqrt{2} , \sqrt{2} - 1) \, $ B). $ ( 1-\sqrt{2} , \sqrt{2} - 1) \, $
C). $ ( 1+\sqrt{2} , \sqrt{2} + 1) \, $ D). $ ( 1-\sqrt{2} , \sqrt{2} - 2) \, $
E). $ ( 1+\sqrt{2} , \sqrt{2} + 2) $
Persamaan lingkaran dengan titik pusat berada pada kurva $ x = y^2 $ dan menyinggung sumbu
Y adalah ...
A). $ x^2 + y^2 - 2b^2x - 2by + b^2 = 0 $
B). $ x^2 + y^2 - 2b^2x - 2by - b^2 = 0 $
C). $ x^2 + y^2 - 2b^2x - 2by + b^4 = 0 $
D). $ x^2 + y^2 - 2b^2x - 2by - b^4 = 0 $
E). $ x^2 + y^2 - 2b^2x - 2by + b^2 + b^4 = 0 $
Nomor 48. Soal UM UNDIP 2018 Matipa A). $ x^2 + y^2 - 2b^2x - 2by + b^2 = 0 $
B). $ x^2 + y^2 - 2b^2x - 2by - b^2 = 0 $
C). $ x^2 + y^2 - 2b^2x - 2by + b^4 = 0 $
D). $ x^2 + y^2 - 2b^2x - 2by - b^4 = 0 $
E). $ x^2 + y^2 - 2b^2x - 2by + b^2 + b^4 = 0 $
Lingkaran yang sepusat dengan lingkaran $ x^2 + y^2 - 6x + 4y - 13 = 0 $ dan
menyinggung garis $ 3x + 4y + 9 = 0 $ mempunyai persamaan ...
A). $ x^2 + y^2 - 6x + 4y - 12 = 0 \, $
B). $ x^2 + y^2 - 6x + 4y - 3 = 0 \, $
C). $ x^2 + y^2 - 6x + 4y + 4 = 0 \, $
D). $ x^2 + y^2 - 6x + 4y + 9 = 0 \, $
E). $ x^2 + y^2 - 6x + 4y + 12 = 0 \, $
Nomor 49. Soal UM UGM 2018 Matipa kode 275 A). $ x^2 + y^2 - 6x + 4y - 12 = 0 \, $
B). $ x^2 + y^2 - 6x + 4y - 3 = 0 \, $
C). $ x^2 + y^2 - 6x + 4y + 4 = 0 \, $
D). $ x^2 + y^2 - 6x + 4y + 9 = 0 \, $
E). $ x^2 + y^2 - 6x + 4y + 12 = 0 \, $
Diberikan garis $ y = \frac{x}{3} $ dan $ y = 3x $. Persamaan lingkaran yang
menyinggung dua garis tersebut, berpusat di $ (-a,-a) $ , $ a > 0 $ , dan
berjari-jari $ \frac{6}{\sqrt{10}} $ adalah ...
A). $ x^2+y^2+6x+6y+\frac{72}{5} = 0 \, $
B). $ x^2+y^2+6x+6y+\frac{82}{5} = 0 \, $
C). $ x^2+y^2+8x+8y+\frac{72}{5} = 0 \, $
D). $ x^2+y^2+9x+9y+\frac{62}{5} = 0 \, $
E). $ x^2+y^2+9x+9y+\frac{82}{5} = 0 \, $
Nomor 50. Soal UM UGM 2018 Matipa kode 576 A). $ x^2+y^2+6x+6y+\frac{72}{5} = 0 \, $
B). $ x^2+y^2+6x+6y+\frac{82}{5} = 0 \, $
C). $ x^2+y^2+8x+8y+\frac{72}{5} = 0 \, $
D). $ x^2+y^2+9x+9y+\frac{62}{5} = 0 \, $
E). $ x^2+y^2+9x+9y+\frac{82}{5} = 0 \, $
Diberikan lingkaran pada bidang koordinat yang memotong sumbu X di $ (1,0) $ dan
$ (3,0) $ . Jika lingkaran tersebut menyinggung sumbu Y, maka titik singgung
yang mungkin adalah ...
A). $ (0,1) \, $ B). $ (0,2) \, $ C). $ (0,\sqrt{3}) $ D). $ (0,\sqrt{5}) \, $ E). $ (0,3) $
A). $ (0,1) \, $ B). $ (0,2) \, $ C). $ (0,\sqrt{3}) $ D). $ (0,\sqrt{5}) \, $ E). $ (0,3) $
Untuk kumpulan soal utbk 2019 matematika saintek dan matematika soshum, silahkan kunjungi link berikut:
Kumpulan Soal UTBK 2019 Matematika Saintek
Kumpulan Soal UTBK 2019 Matematika Soshum





