Kumpulan Soal Integral Seleksi Masuk PTN

         Blog koma - Artikel berikut ini masih berkaitan dengan "Kumpulan Soal Matematika Per Bab Seleksi Masuk PTN" yaitu Kumpulan Soal Integral Seleksi Masuk PTN yang merupakan kumpulan soal-soal integral dari berbagai jenis seleksi masuk PTN seperti SBMPTN, SNMPTN, SPMB, UMPTN, dan seleksi mandiri seperti Simak UI, UM UGM atau UTUL UGM, dan lainnya, serta yang kita susun dari kumpulan beberapa tahun, tentunya akan kami update secara berkala kumpulan soal-soalnya. Kumpulan Soal Integral Seleksi Masuk PTN diharapkan akan memudahkan bagi teman-teman dalam belajar dan fokus untuk pendalaman materi integral. Materi integral terdiri dari integral fungsi aljabar dan sifatnya, integral fungsi trigonometri, luasan daerah, dan volume benda putar. Langsung saja berikut Kumpulan Soal Integral Seleksi Masuk PTN yang dilengkapi pembahasannya.

Nomor 1. Soal SBMPTN Mat IPA 2014 Kode 554

Jika $C(t)=\frac{1}{t} \int \limits_0^t \left( f(s)+g(s) \right) ds$ dan $\displaystyle \lim_{a \to 0} \frac{C(t_0+a)-C(t_0)}{a}=0$, maka $C(t_0)=...$

Nomor 2. Soal SBMPTN Mat IPA 2014 Kode 554

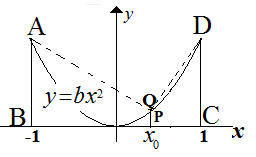
Misalkan $A(t)$ menyatakan luas daerah di bawah kurva $y=bx^2 , 0\leq x \leq t$. Jika titik $P(x_0,0)$ sehingga $A(x_0):A(1)=1:8$, maka perbandingan luas trapesium $ABPQ:DCPQ=...$

Nomor 3. Soal SBMPTN Mat IPA 2014 Kode 514

Jika $f(x)=1+sinx+sin^2x+sin^3x+..., \, 0 \leq x \leq \frac{\pi}{4}$, maka $\int \limits_0^{\frac{\pi}{4}} f(x) dx = ...$

Nomor 4. Soal UM-UGM Mat IPA 2014

Diketahui $D_1$ adalah daerah di kuadran I yang dibatasi oleh parabola $y=\frac{9}{4}x^2$ , parabola $y=x^2$ , dan garis $x=2$ , dan $D_2$ daerah yang dibatasi oleh garis $x=2$ , garis $y=9$ , dan parabola $y=x^2$ . Jika luas $D_1=a$ , maka luas $D_2$ adalah ...

Nomor 5. Soal SBMPTN Mat IPA 2013 Kode 436

$\int 8\sin ^2 x \cos ^2 x dx = ...$

Nomor 6. Soal SBMPTN Mat IPA 2013 Kode 436

Jika $L(a)$ adalah luas daerah yang dibatasi oleh sumbu X dan parabola $y=ax-x^2, \, 0 < a < 1,$ maka peluang nilai $a$ sehingga $L(a) \geq \frac{1}{12}$ adalah ...

Nomor 7. Soal SBMPTN Mat IPA 2013 Kode 436

Luas daerah yang dibatasi oleh kurva $y=x^2-4$ dan $y=-3|x|$ adalah ...

Nomor 8. Soal SPMK UB Mat IPA 2013

Misalkan $f(x)=\int \limits_0^x (as+b)ds $ . Jika $f(-1)=1 $ dan $f(1)=3 $ , maka $ab = ... $

Nomor 9. Soal SNMPTN Mat IPA 2012 Kode 634

Luas daerah yang dibatasi oleh kurva $y=x^2 $ , $ y=1 $ , dan $ x=2 $ adalah ...

Nomor 10. Soal SNMPTN Mat IPA 2011 Kode 574

Pernyataan berikut yang benar adalah ...
(A) Jika $\sin x = \sin y $ , maka $x=y$
(B) Untuk setiap vektor $\vec{u}, \vec{v} $ dan $\vec{w} $ berlaku $\vec{u}.(\vec{v}.\vec{w}) = (\vec{u}.\vec{v}).\vec{w} $
(C) Jika $\int \limits_a^b f(x)dx=0 $ , maka $f(x) = 0 $
(D) Ada fungsi $f$ sehingga $\displaystyle \lim_{x \to c} f(x) \neq f(c) $ untuk suatu $c$
(E) $1-\cos 2x = 2\cos ^2 x $

Nomor 11. Soal SNMPTN Mat IPA 2011 Kode 574

Luas daerah di bawah $y=-x^2+8x$ , di atas $y=6x-24 $ , dan terletak di kuadran I adalah ...

Nomor 12. Soal SNMPTN Mat IPA 2010 Kode 526

Daerah R di kuadran satu, dibatasi oleh grafik $y=x^2, \, y=x+2 $ dan $y=0 $ . Integral yang menyatakan luas daerah R adalah ...

Nomor 13. Soal SNMPTN Mat IPA 2009 Kode 276

Jika pada $\int \limits_{-1}^2 x^2\sqrt{x+1} dx $ disubstitusikan $ u = x +1 $ , maka menghasilkan ....

Nomor 14. Soal SNMPTN Mat IPA 2009 Kode 276

Jika nilai $\int \limits_{1}^2 f(x) dx = 6 $ , maka nilai $\int \limits_{0}^1 xf(x^2+1) dx $ adalah ....

Nomor 15. Soal SNMPTN Mat IPA 2008 Kode 302

Luas daerah yang dibatasi oleh $y=2 \sin x , \, x = \frac{\pi}{2} , \, x = \frac{3\pi}{2} $ , dan sumbu X sama dengan ....

Nomor 16. Soal SPMB Mat IPA 2007

Luas daerah dibatasi oleh grafik fungsi-fungsi $ y = \sin x , \, y = \cos x \, $ dan sumbu X untuk $ 0 \leq x \leq \frac{\pi}{2} \, $ adalah ....

Nomor 17. Soal SPMB Mat IPA 2006

$ 15 \int \limits_2^3 x\sqrt{x-2} dx = .... $

Nomor 18. Soal Selma UM Mat IPA 2014

Integral yang menyatakan luas daerah di kuadran pertama yang dibatasi oleh kurva $ \, y = \frac{1}{x} \, $ , garis $ \, y = x, \, $ garis $ \, x = 2, \, $ dan sumbu X adalah ....

Nomor 19. Soal SPMB Mat IPA 2005

Jika $ f(x) = \int \cos ^2 x \, dx \, $ dan $ \, g(x) = xf^\prime (x), \, $ maka $ \, g^\prime \left( x - \frac{\pi}{2} \right) = .... $

Nomor 20. Soal SPMB Mat IPA 2004

$ \int \limits_{-3}^{3} | x^2 - 2x - 3 | \, dx = .... $

Nomor 21. Soal SPMB Mat IPA 2003

Luas daerah dalam kuadran I yang dibatasi oleh $ y = 4 - x^2, \, y = 3x \, $ dan $ y = 0, \, $ dapat dinyatakan sebagai ....

Nomor 22. Soal SPMB Mat IPA 2003

Diketahui $ \int f(x)dx = ax^2 + bx + c \, $ dan $ a \neq 0 \, $. Jika $ a, \, f(a), \, 2b \, $ merupakan barisan aritmetika, dan $ f(b) = 6 , $ maka $ \int \limits_0^1 f(x) dx = .... $

Nomor 23. Soal SPMB Mat IPA 2002

Daerah $ D $ dibatasi oleh grafik fungsi $ y = \frac{1}{\sqrt{x}} , \, $ garis $ x = 1, \, $ garis $ x = 4, \, $ dan sumbu X. Jika garis $ x = c \, $ memotong daerah $ D $ sehingga menjadi daerah $ D_1 $ dan $ D_2 $ yang luasnya sama, maka $ c = .... $

Nomor 24. Soal UMPTN Mat IPA 2001

Daerah D dibatasi oleh urva $ y = \sin x , \, 0 \leq x \leq \pi \, $ dan sumbu X. Jika daerah D diputar terhadap sumbu X, maka volume benda putar yang terjadi adalah ....

Nomor 25. Soal UMPTN Mat IPA 2000

Gradien garis singgung suatu kurva di titik ($x,y$) adalah $ 3\sqrt{x} $ . Jika kurva ini melalui titik (4,9), maka persamaan garis singgung kurva ini di titik berabsis 1 adalah ....

Nomor 26. Soal SPMK UB Mat IPA 2014

$\int \frac{3x}{\left( 3x^2 + 1 \right)^2} dx = ...$

Nomor 27. Soal SPMK UB Mat IPA 2014

Daerah $D$ dibatasi oleh grafik $y = x^2$ dan $y = 2x^2 - 1$. Luas daerah $D$ dapat dinyatakan sebagai ...

Nomor 28. Soal SPMK UB Mat IPA 2009

Petunjuk C digunakan untuk menjawab soal nomor 12 sampai 15.
Diketahui $ f(x) = \int \limits_a^x t \, dt \, $ dengan $ a > 0 \, $ . Jika $ f(2)=0, \, $ maka kurva tersebut memotong sumbu X pada titik ....
(1). (-4,0)       (2). (2,0)       (3). (4,0)       (4). (-2,0)

Nomor 29. Soal SPMK UB Mat IPA 2008

Luas daerah yang dibatasi oleh garis $ y = x-1 \, $ dan parabola $ y^2 = 2x + 6 \, $ adalah .... satuan.

Nomor 30. Soal SBMPTN Mat IPA 2015 Kode 517

Pada interval $ -2 \leq x \leq 2 , \, $ luas daerah di bawah kurva $ y = 4 - x^2 \, $ dan di atas garis $ y = k \, $ sama dengan luas daearah di atas kurva $ y = 4 - x^2 \, $ dan di bawah garis $ y = k. \, $ Nilai $ k = .... $

Nomor 31. Soal SPMK UB Mat IPA 2015

Luas daerah A yang dibatasi oleh grafik $ y = x^2, \, y = x^2 - 20x + 100 \, $ dan $ y = 0 \, $ dapat dinyatakan sebagai ...
A). $ \int \limits_0^{10} (2x^2 - 20x + 100) dx $
B). $ \int \limits_0^{10} ( 20x - 100) dx $
C). $ \int \limits_0^{5} x^2 dx - \int \limits_5^{10} ( 20x - 100) dx $
D). $ \int \limits_0^{5} x^2 dx + \int \limits_0^{10} ( x^2 - 20x + 100) dx $
E). $ \int \limits_0^{5} x^2 dx + \int \limits_5^{10} ( x^2 - 20x + 100) dx $

Nomor 32. Soal UTUL UGM Mat IPA 2016 Kode 581

Luas daerah yang dibatasi oleh kurva $ y = 2 \cos x , \, y = 1, \, $ sumbu X dan sumbu Y adalah ....
A). $ \frac{\pi}{6} + \int \limits_\frac{\pi}{3}^\frac{\pi}{2} \, 2 \cos x \, dx $
B). $ \frac{\pi}{3} + \int \limits_\frac{\pi}{6}^\frac{\pi}{2} \, 2 \cos x \, dx $
C). $ \frac{\pi}{3} + \int \limits_\frac{\pi}{3}^\frac{\pi}{2} \, 2 \cos x \, dx $
D). $ \frac{\pi}{2} + \int \limits_\frac{\pi}{3}^\frac{\pi}{2} \, 2 \cos x \, dx $
E). $ \frac{\pi}{2} + \int \limits_\frac{\pi}{6}^\frac{\pi}{2} \, 2 \cos x \, dx $

Nomor 33. Soal UTUL UGM Mat IPA 2016 Kode 381

$ \int \limits_\frac{1}{2}^1 \left( \sqrt[3]{2x-1} + \sin \pi x \right) \, dx = .... $
A). $ \frac{3\pi - 8}{8\pi} $
B). $ \frac{3\pi - 4}{4\pi} $
C). $ \frac{3\pi + 4}{4\pi} $
D). $ \frac{3\pi + 8}{8\pi} $
E). $ \frac{3}{4} + \pi $

Nomor 34. Soal SBMPTN Mat IPA 2016 Kode 245

Diketahui fungsi $ f(x) = f(x+2) $ untuk setiap $ x $. Jika $ \int \limits_0^2 f(x) \, dx = B $, maka $ \int \limits_3^7 f(x+8) \, dx = .... $
A). $ B \, $ B). $ 2B \, $ C). $ 3B \, $ D). $ 4B \, $ E). $ 5B $

Nomor 35. Soal SBMPTN Mat IPA 2016 Kode 245

Misalkan D adalah daerah yang dibatasi oleh sumbu-Y, daris $ y = 4$, dan kurva $ y = x^2$. Jika garis $ y = k $ membagi dua daerah D sama besar, maka $ k^3 = .... $
A). $ 8 \, $ B). $ 9 \, $ C). $ 11 \, $ D). $ 14 \, $ E). $ 16 $

Nomor 36. Soal SBMPTN Mat IPA 2016 Kode 246

Luas daerah di antar kurva $ y = -3a+4 $ dan kurva $ y = x^2-3a $ selalu bernilai konstan, yaitu $ k$. Nilai $ k $ adalah ....
A). $ \frac{34}{3} \, $ B). $ \frac{32}{3} \, $ C). $ \frac{28}{3} \, $ D). $ \frac{16}{3} \, $ E). $ \frac{8}{3} $

Nomor 37. Soal SBMPTN Mat IPA 2016 Kode 247

Diketahui fungsi $ f $ dan $ g $ dengan $ f(x) = f(x+a) $ , $ f(x) = x^5 + 2016x^3 \, $ untuk $ 0 < x < a $ , dan $ g(x) = g(x+2a) $ , $ g(x) = x^5 + 2016x^3 \, $ untuk $ -a < x \leq a $ , dan $ \int \limits_0^a f(x) dx = b $. Nilai dari $ \int \limits_0^{3a} (f(x) + g(x)) dx $ adalah ....
A). $ 2a \, $ B). $ 3a \, $ C). $ 4b \, $ D). $ 5b \, $ E). $ 6b $

Nomor 38. Soal SBMPTN Mat IPA 2016 Kode 249

Diketahui fungsi $ f(x) = x^2 $ dan $ g(x) = ax, \, a >0 $. Misalkan D adalah daerah yang dibatasi oleh kurva $ f $ dan $ y = 4 $. Jika kurva $ g $ membagi daerah D dengan perbandingan luas $ 1 : 7 $, maka $ a = .... $
A). $ 1 \, $ B). $ 2 \, $ C). $ 3 \, $ D). $ 4 \, $ E). $ 5 $

Nomor 39. Soal SBMPTN Mat IPA 2016 Kode 250

Luas daerah di antar kurva $ y = 2a + 1 $ dan kurva $ y = x^2+2a $ selalu bernilai konstan, yaitu $ k$. Nilai $ k $ adalah ....
A). $ \frac{1}{3} \, $ B). $ \frac{2}{3} \, $ C). $ \frac{4}{3} \, $ D). $ \frac{5}{3} \, $ E). $ \frac{7}{3} $

Nomor 40. Soal SBMPTN Mat IPA 2016 Kode 252

Misalkan D adalah daerah yang dibatasi oleh sumbu-Y, daris $ y = 8$, dan kurva $ y = x^3$. Jika garis $ y = k $ membagi dua daerah D sama besar, maka $ k^4 = .... $
A). $ 2^5 \, $ B). $ 2^7 \, $ C). $ 2^8 \, $ D). $ 2^9 \, $ E). $ 2^{10} $

Nomor 41. Soal SBMPTN Mat IPA 2016 Kode 252

Nilai $ k $ antara $ 0 $ dan $ \pi $ yang membuat $ \int_0^k \sin ^2 x \cos x dx \, $ maksimum adalah ....
A). $ \frac{\pi}{6} \, $ B). $ \frac{\pi}{5} \, $ C). $ \frac{\pi}{4} \, $ D). $ \frac{\pi}{3} \, $ E). $ \frac{\pi}{2} $

Nomor 42. Soal SBMPTN Mat IPA 2017 Kode 165

Jika $ \int_{-4}^4 f(x) (\sin x + 1) dx = 8 $ , dengan $ f(x) $ fungsi genap dan $ \int_{-2}^4 f(x) dx = 4 $ , maka $ \int_{-2}^0 f(x) dx = .... $
A). $ 0 \, $ B). $ 1 \, $ C). $ 2 \, $ D). $ 3 \, $ E). $ 4 $

Nomor 43. Soal SBMPTN MatDas 2017 Kode 224

$ \int \frac{1-x}{\sqrt{x}} dx = .... $
A). $ \frac{3}{2}(3+x)\sqrt{x} + C \, $
B). $ \frac{2}{3}(3-x)\sqrt{x} + C \, $
C). $ \frac{2}{3}(3+\sqrt{x})x + C \, $
D). $ \frac{1}{3\sqrt{x}} \left( \frac{1}{x} - 1 \right) + C \, $
E). $ \frac{1}{2\sqrt{x}} \left( \frac{1}{x} + 1 \right) + C $

Nomor 44. Soal SBMPTN MatDas 2017 Kode 265

$ \int \frac{x}{\sqrt{x^2 + 3}} dx = .... $

Nomor 45. Soal SBMPTN MatDas 2017 Kode 268

$ \int 9x^2 \sqrt{8-x^3} dx = .... $

Nomor 46. Soal UTUL UGM Mat IPA 2017 Kode 713

Jika daerah yang dibatasi oleh kurva $ y = x^2 $ dan garis $ y = (2m-2)x $ mempunyai luas $ 1\frac{1}{3} $ , maka $ m = .... $
A). $ 2\frac{1}{2} \, $ atau $ -\frac{1}{2} $
B). $ 2 \, $ atau $ 0 $
C). $ 3\frac{1}{2} \, $ atau $ -1\frac{1}{2} $
D). $ 4 \, $ atau $ -2 $
E). $ 4\frac{1}{2} \, $ atau $ -2\frac{1}{2} $

Nomor 47. Soal SBMPTN MatDas 2017 Kode 207

$ \int \frac{x+1}{\sqrt{x^2 + 2x}} dx = .... $

Update bulan November 2017 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya.

Nomor 48. Soal UM Undip 2016 Mat dasar IPA

$ \int x^5 \left( 2 - x^3 \right) ^\frac{1}{2} \, dx = .... $
A). $ \frac{2}{45}(3x^3+4)(-x^3+2)^\frac{3}{2} + c \, $
B). $ \frac{-2}{5}(3x^3+4)(-x^3+2)^\frac{3}{2} + c \, $
C). $ \frac{2}{5}(3x^3+4)(-x^3+2)^\frac{3}{2} + c \, $
D). $ \frac{-2}{25}(3x^3+4)(-x^3+2)^\frac{3}{2} + c \, $
E). $ \frac{-2}{45}(3x^3+4)(-x^3+2)^\frac{3}{2} + c \, $

Nomor 49. Soal UM Undip 2016 Mat dasar IPA

Luas daerah yang dibatasi oleh parabola $ y = \sqrt{x} + 1 $ dan garis-garis singgungnya melalui titik $\left( 0, \frac{3}{2} \right) $ adalah ... satuan luas.
A). $ \frac{2}{3}\sqrt{2} \, $ B). $ \frac{2}{3} \, $ C). $ \frac{2}{3}\sqrt{3} \, $ D). $ \frac{1}{12} \, $ E). $ \frac{1}{3}\sqrt{2} $

Nomor 50. Soal UM Undip 2016 Mat dasar IPA

Volume benda putar jika luas daerah yang dibatasi oleh kurva $ y = \sqrt{x-1} $ dan $ y = x^2 - 2x + 1 $ diputar terhadap garis $ x = 2 $ sama dengan ... satuan volume.
A). $ \frac{3}{10}\pi \, $ B). $ \frac{1}{3}\pi \, $ C). $ \frac{2}{5}\pi \, $ D). $ \frac{11}{30}\pi \, $ E). $ \frac{3}{5}\pi $

Nomor 51. Soal UM UGM 2009 Mat IPA

Jika $ \int \limits_1^2 \frac{1}{\sqrt{x} + 1} \, dx = a $, maka $ \int \limits_1^2 \frac{4\sqrt{x} + k}{\sqrt{x} + 1} \, dx = 4 - 3a \, $ untuk $ k = .... $
A). $ -3 \, $ B). $ -2 \, $ C). $ -1 \, $ D). $ 1 \, $ E). $ 2 $

Nomor 52. Soal UM UGM 2008 Mat IPA

Jika luas daerah yang dibatasi oleh kurva $ y = x^2 $ dan garis $ y = (2m-1)x $ adalah $ 4\frac{1}{2} $ , maka $ m = .... $
A). $ 1\frac{1}{2} \, $ atau $ -\frac{1}{2} $
B). $ 2 \, $ atau $ -1 $
C). $ 2\frac{1}{2} \, $ atau $ -1\frac{1}{2} $
D). $ 3 \, $ atau $ -2 $
E). $ 3\frac{1}{2} \, $ atau $ -2\frac{1}{2} $

Nomor 53. Soal UM UGM 2008 Mat IPA

Gradien garis singgung suatu kurva di titik $ (x,y) $ sama dengan $ 2x + 5 $. Jika kurva ini melalui titk $(2,20) $ , maka kurva tersebut memotong sumbu X di titik ....
A). $ (2,0) \, $ dan $ (3,0) $
B). $ (-2,0) \, $ dan $ (-3,0) $
C). $ (2,0) \, $ dan $ (-3,0) $
D). $ (-2,0) \, $ dan $ (3,0) $
E). $ (-2,0) \, $ dan $ (2,0) $

Nomor 54. Soal UM UGM 2007 Mat IPA

Perhatikan gambar di atas. Jika $ P\left( \frac{3}{2}, \frac{1}{2} \right) $ maka luas daerah terarsir adalah ....
A). $ \frac{1}{6} \, $ B). $ \frac{1}{3} \, $ C). $ \frac{5}{8} \, $ D). $ \frac{2}{3} \, $ E). $ \frac{3}{4} $

Nomor 55. Soal UM UGM 2006 Mat IPA

Luas daerah yang diarsir di bawah adalah ....

A). $ \frac{\pi}{6} + \int \limits_\frac{\pi}{3}^\frac{\pi}{2} 2\cos x dx \, $
B). $ \frac{\pi}{3} + \int \limits_\frac{\pi}{6}^\frac{\pi}{2} 2\cos x dx \, $
C). $ \frac{\pi}{3} + \int \limits_\frac{\pi}{3}^\frac{\pi}{2} 2\cos x dx \, $
D). $ \frac{\pi}{2} + \int \limits_\frac{\pi}{3}^\frac{\pi}{2} 2\cos x dx \, $
E). $ \frac{\pi}{2} + \int \limits_\frac{\pi}{6}^\frac{\pi}{2} 2\cos x dx \, $

Nomor 56. Soal UM UGM 2004 Mat IPA

Jika D daerah dikuadran I yang dibatasi oleh parabola $ y^2 = 2x $ dan garis $ x - y = 4 $, maka luas D = ....
A). $ 40\sqrt{2} \, $ B). $ 40 \, $ C). $ \frac{64\sqrt{2}}{3} \, $ D). $ \frac{64}{3} \, $ E). $ 13\frac{1}{3} \, $

Nomor 57. Soal UM UGM 2003 Mat IPA

Luas bagian bidang yang dibatasi oleh sumbu Y, kurva $ y = \cos 3x $ dan $ y = \sin 3x $ adalah ....
A). $ \frac{1}{2}(\sqrt{3} + 1) \, $ B). $ \frac{1}{2}(\sqrt{3} - 1) \, $
C). $ \frac{1}{3}(\sqrt{2} - 1) \, $ D). $ \frac{1}{3}(\sqrt{3} + 1) \, $
E). $ \frac{1}{6}(\sqrt{3}- \sqrt{2}) $

Nomor 58. Soal SBMPTN 2017 MatDas Kode 233

$ \int \frac{3(1-x)}{1 + \sqrt{x}} dx = .... $
A). $ 3x - 2x\sqrt{x} + C \, $
B). $ 2x - 3x\sqrt{x} + C \, $
C). $ 3x\sqrt{x} - 2x + C \, $
D). $ 2x\sqrt{x} - 3x + C \, $
E). $ 3x + 2x\sqrt{x} + C $

Nomor 59. Soal UM UNDIP 2017 Mat IPA

Luas daerah yang dibatasi oleh setengah lingkaran atas $ x^2 + y^2 = 4 $ dan parabola $ y = x^2 - 4 $ sama dengan .... satuan luas.
A). $ 2\pi + 10\frac{2}{3} \, $ B). $ 2\pi + 9\frac{2}{3} \, $
C). $ 2\pi + 8\frac{2}{3} \, $ D). $ 2\pi + 7\frac{2}{3} \, $
E). $ 2\pi + 6\frac{2}{3} $

Nomor 60. Soal UM UNDIP 2017 Mat IPA

$ \int \frac{x^3}{2\sqrt{x-1}} + 3x^2 \sqrt{x-1} \, dx = .... $
A). $ x^2\sqrt{x-1} + c \, $
B). $ x\sqrt{x-1} + c \, $
C). $ x^3\sqrt{x-1} + \frac{1}{\sqrt{x-1}} + c \, $
D). $ x^3\sqrt{x-1} + c \, $
E). $ x^3\sqrt{x-1} - \sqrt{x-1} + c $

Update bulan Desember 2018 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya.

Nomor 61. Soal SBMPTN 2017 MatDas Kode 202

$ \int \frac{x - 4}{ \sqrt{x} + 2} dx = .... $
A). $ \frac{3}{2}x\sqrt{x} - 2x + C \, $
B). $ \frac{3}{2}x\sqrt{x} + 2x + C \, $
C). $ x\sqrt{x} + 2x + C \, $
D). $ \frac{2}{3}x\sqrt{x} - 2x + C \, $
E). $ \frac{2}{3}x\sqrt{x} + 2x + C $

Nomor 62. Soal SBMPTN 2017 MatDas Kode 232

$ \int \, \sqrt{x} \left( x^2 - \frac{1}{x^2} \right) dx = .... $
A). $ \frac{2}{7}x^3\sqrt{x} + \frac{2}{\sqrt{x}} + C \, $
B). $ \frac{2}{7}x^3\sqrt{x} + \frac{1}{\sqrt{x}} + C \, $
C). $ \frac{2}{7}x^3\sqrt{x} + \frac{1}{2\sqrt{x}} + C \, $
D). $ \frac{2}{7}x^3\sqrt{x} - \frac{2}{\sqrt{x}} + C \, $
E). $ \frac{2}{7}x^3\sqrt{x} - \frac{1}{2\sqrt{x}} + C $

Nomor 63. Soal SBMPTN 2018 Matipa Kode 452

Daerah R dibatasi oleh $ y= \sqrt{x} $ , $ y = -x + 6 $ , dan sumbu $ x $. Volume benda padat yang didapat dengan memutar R terhadap sumbu $ x $ adalah ....
A). $ \frac{8\pi}{3} \, $ B). $ \frac{16\pi}{3} \, $ C). $ \frac{24\pi}{3} \, $ D). $ \frac{32\pi}{3} \, $ E). $ \frac{40\pi}{3} $

Nomor 64. Soal SBMPTN 2018 Matipa Kode 452

Nilai $ \int \limits_0^1 15x \sqrt{1-x} dx $ adalah .....
A). $ 1 \, $ B). $ 2 \, $ C). $ 3 \, $ D). $ 4 \, $ E). $ 5 $

Nomor 65. Soal SBMPTN 2018 Matdas Kode 517

$ \int \left( \frac{-16-6x^4}{x^2} \right) dx = .... $
A). $ \frac{16}{x} + 2x^3 + C \, $
B). $ \frac{16}{x} - 2x^3 + C \, $
C). $ -\frac{16}{x} - x^3 + C \, $
D). $ -\frac{8}{x} + 2x^3 + C \, $
E). $ \frac{8}{x} - 2x^3 + C $

Nomor 66. Soal SBMPTN 2018 Matdas Kode 526

$ \int \left( 2x - \frac{1}{2x} \right)^2 dx = .... $
A). $ \frac{2}{3}x^3 - \frac{1}{2x} - 2x + C \, $
B). $ \frac{2}{3}x^3 + \frac{1}{2x} - 2x + C \, $
C). $ \frac{4}{3}x^3 - \frac{1}{2x} + 2x + C \, $
D). $ \frac{4}{3}x^3 - \frac{1}{4x} - 2x + C \, $
E). $ \frac{4}{3}x^3 + \frac{1}{4x} - 2x + C $

Nomor 67. Soal SBMPTN 2018 Matdas Kode 550

$ \int \sqrt{ x^4 + \frac{1}{x^4} + 2 } \, dx = .... $
A). $ \frac{1}{3}x^3 - \frac{1}{x} + C \, $
B). $ -\frac{1}{3}x^3 - \frac{1}{x} + C \, $
C). $ \frac{1}{3}x^3 + \frac{1}{x} + C \, $
D). $ -\frac{1}{3}x^3 + \frac{1}{x} + C \, $
E). $ \frac{1}{3}x^3 + \frac{1}{x} + C $

Nomor 68. Soal SBMPTN 2018 Matdas Kode 552

$ \int \left( \frac{x^4-1}{x^3 + x} \right)^2 dx = .... $
A). $ \frac{1}{3}x^3 + \frac{1}{x} - 2x + C \, $
B). $ \frac{1}{3}x^3 - \frac{1}{x} - 2x + C \, $
C). $ \frac{1}{3}x^3 + \frac{1}{x} + 2x + C \, $
D). $ \frac{1}{3}x^3 - \frac{1}{x} + x + C \, $
E). $ \frac{1}{3}x^3 - \frac{1}{x} - x + C $

Nomor 69. Soal UM UNDIP 2018 Matipa

Diketahui suatu kurva melalui titik $ \left( -1, -\frac{1}{3} \right)$. Jika kemiringannya pada setiap titik $ x $ adalah kebalikan negatif dari kemiringan kurva dengan persamaan $ xy = 2 $ , maka persamaan kurva tersebut adalah ...
A). $ 6y - x^3 + 1 = 0 \, $
B). $ 12y - 3x^3 + 1 = 0 \, $
C). $ 3y - x^3 = 0 \, $
D). $ 6y - 3x^3 = 0 \, $
E). $ 15y - 3x^3 + 2 = 0 \, $

Nomor 70. Soal UM UNDIP 2018 Matipa

Luas daerah yang dibatasi oleh sumbu Y, kurva $ y = -x^2 + 2x $ dan garis singgung kurva di titik $ (2,0) $ sama dengan ...
A). $ 1\frac{1}{2} \, $ B). $ 1\frac{2}{3} \, $ C). $ 2\frac{1}{3} \, $ D). $ 2\frac{1}{2} \, $ E). $ 2\frac{2}{3} $

       Demikian Kumpulan Soal Integral Seleksi Masuk PTN lengkap dengan pembahasannya. Semoga artikel ini bermanfaat untuk kita semua. Kumpulan Soal Integral Seleksi Masuk PTN ini akan terus kami update untuk soal-soal tahun lainnya. Jika ada kritik dan saran, langsung saja ketikkan komentar pada kolom kontar di bagian bawah setiap artikel. Silahkan juga pelajari kumpulan soal lain pada "Kumpulan Soal Matematika Per Bab Seleksi Masuk PTN". Terima Kasih.

       Untuk kumpulan soal utbk 2019 matematika saintek dan matematika soshum, silahkan kunjungi link berikut:
Kumpulan Soal UTBK 2019 Matematika Saintek
Kumpulan Soal UTBK 2019 Matematika Soshum