Untuk memudahkan mempelajari soal-soal dalam Kumpulan Soal Dimensi Tiga Seleksi Masuk PTN ini, tentu teman-teman harus menguasai terlebih dahulu materi yang berkaitan dengan dimensi tiga. Hal-hal yang sering ditanyakan dalam soal-soal dimensi tiga adalah jarak dan sudut yang tentu terkait dengan trigonometri juga. Berikut Kumpulan Soal Dimensi Tiga Seleksi Masuk PTN beserta lengkap dengan pembahasannya.
Nomor 1. Soal SBMPTN Mat IPA 2014 Kode 554

Diketahui kubus ABCD.EFGH dengan titik X terletak pada rusuk EF sejauh 2 cm dari F dan Y adalah titik potong perpanjangan AX dan perpanjangan BF. Jika panjang rusuk kubus tersebut 6 cm, maka jarak Y ke G adalah .... cm.
A). $ 2\sqrt{6} \, $ B). $ 3\sqrt{3} \, $ C). $ 3\sqrt{5} \, $ D). $ 2\sqrt{17} \, $ E). $ 3\sqrt{13} $
Nomor 43. Soal SBMPTN MatDas 2017 Kode 265

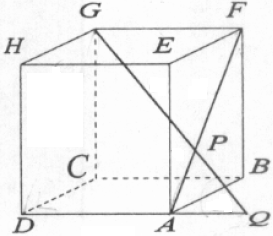
Diketahui kubus ABCD.EFGH dengan P adalah titik tengah BF dan Q adalah titik potong AP dan BE seperti pada gambar. Jika rusuk kubus tersebut adalah 6 cm, maka jarak Q ke H adalah .... cm
A). $ 3\sqrt{13} \, $ B). $ 2\sqrt{17} \, $ C). $ 3\sqrt{3} \, $ D). $ 2\sqrt{6} \, $ E). $ 4 \, $
Nomor 44. Soal SBMPTN MatDas 2017 Kode 268

Diketahui kubus ABCD.EFGH dengan M dan N berturut-turut adalah titik tengah FG dan BC, serta T adalah titik pada AM sehingga NT tegak lurus AM seperti pada gambar. Jika panjang rusuk kubus tersebut 8 cm, maka panjang NT adalah ... cm.
Nomor 47. Soal UTUL UGM Mat IPA 2017 kode 814
Nomor 48. Soal UM Undip 2016 Mat dasar IPA
Update bulan Desember 2018 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya.
Nomor 58. Soal SBMPTN 2017 MatDas Kode 226
Demikian Kumpulan Soal Dimensi Tiga Seleksi Masuk PTN lengkap dengan pembahasannya. Semoga artikel ini bermanfaat untuk kita semua.
Kumpulan Soal Dimensi Tiga Seleksi Masuk PTN ini akan terus kami update untuk soal-soal tahun lainnya. Jika ada kritik dan saran, langsung saja ketikkan
komentar pada kolom kontar di bagian bawah setiap artikel. Silahkan juga pelajari kumpulan soal lain pada "Kumpulan Soal Matematika Per Bab Seleksi Masuk PTN". Terima Kasih.
Diberikan kubus $ABCD.EFGH$ dengan panjang rusuk $3p$. Titik-titik P, Q, dan R masing-masing pada FB, FG, dan AD sehingga $BP=GQ=DR=p$.
Misalkan $\beta$ adalah irisan bidang yang melalui P, Q, dan R. Luas alas yang berada di bawah bidang $\beta$ adalah ... $p^2$.
Nomor 2. Soal SBMPTN Mat IPA 2014 Kode 514
Diketahui kubus ABCD.EFGH. Titik $P,Q,R$, dan $S$ masing-masing pada $AB, BC, CD$, dan $AD$ sehingga $BP=CR=\frac{AB}{3}$ dan
$QC=DS=\frac{AD}{3}$. Volume limas E.PQRS adalah ... volume kubus.
Nomor 3. Soal UTUL UGM Mat IPA 2014
Sebuah prisma $ABCD.EFGH$ memiliki alas berbentuk persegi. Titik $T$ adalah titik tengah diagonal $HF$ . Jika $\angle EAT=\frac{\pi }{6}$ dan volume prisma tersebut $4\sqrt{6}$
, maka tinggi prisma adalah ...
Nomor 4. Soal SBMPTN Mat IPA 2013 Kode 436
Diketahui kubus ABCD.EFGH mempunyai sisi 4 cm. Titik P pada BC sehingga PB = 1 cm, titik Q pada GH sehingga HQ = 1 cm,
R titik tengah AE. Jarak R ke PQ adalah ...
Nomor 5. Soal SNMPTN MatDas 2010 Kode 336
Balok ABCD.EFGH mempunyai panjang rusuk AB = 4 cm, BC = 3 cm, dan AE = 3 cm. Bidang AFH memotong balok menjadi 2 bagian dengan perbandingan
volumenya adalah ...
Nomor 6. Soal SNMPTN Mat IPA 2012 Kode 634
Diketahui kubus ABCD.EFGH . Jika $\alpha $ adalah sudut antara bidang ACF dan alas ABCD, maka $\tan \alpha = ...$
Nomor 7. Soal SNMPTN Mat IPA 2011 Kode 574
Prisma tegak segitiga sama sisi ABC.DEF dengan panjang AB = $s$ dan AD = $t$ . Jika titik G terletak di tengah-tengah sisi
EF, maka panjang AG adalah ...
Nomor 8. Soal SNMPTN Mat IPA 2010 Kode 526
Diketahui limas beraturan T.ABCD dengan panjang rusuk 6 cm. Titik P pada CT sehingga TP : PC = 2 : 1. Jarak P ke bidang
BDT adalah ...
Nomor 9. Soal SNMPTN Mat IPA 2009 Kode 276
Diketahui kubus ABCD.EFGH . Titik tengah sisi AB, BF, dan FG diberi simbol X, Y, dan Z. Besar sudut $\angle $XYZ adalah ....
Nomor 10. Soal SNMPTN Mat IPA 2008 Kode 302
Satuan limas beraturan T.PQRS dengan TP = TQ = TR = TS = $\sqrt{21} $ dan PQRS adalah suatu persegi dengan panjang sisi
6 cm. Besar sudut antarbidang TQR dan bidang alas sama dengan ....
Nomor 11. Soal Simak UI Mat IPA 2014
Diberikan kubus ABCD.EFGH. Titik R terletak pada rusuk EH sedemikian sehingga ER=3RH dan titik S berada di tengah rusuk FG. Bidang $\Omega$ melalui
titik R, S, dan A. Jika U adalah titik potong antara bidang $\Omega$ dan rusuk BF, dan $\theta$ adalah sudut yang terbentuk antara garis RS dan AU, maka $\tan \theta =...$
Nomor 12. Soal SPMB Mat IPA 2007
Diketahui kubus ABCD.EFGH yang mempunyai panjang rusuk 1 cm. Jarak D ke bidang EBG sama dengan ....
Nomor 13. Soal SPMB Mat IPA 2007
Diberikan ABCD.EFGH. Perbandingan luas permukaan kubus ABCD.EFGH dengan limas H.ACF adalah ....
Nomor 14. Soal SPMB Mat IPA 2006
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jika titik P pada CG dan titik Q pada DH dan CP = DQ = 1 cm, maka bidang PQEF mengiris kuus tersebut menjadi
dua bagian. Volume bagian yang lebih besar adalah .....
Nomor 15. Soal Selma UM Mat IPA 2014
Diketahui kubus ABCD.EFGH dengan panjang rusuk 6 cm. Jarak titik A ke bidang BDE adalah ....
Nomor 16. Soal SPMB Mat IPA 2005
Diketahui kubus ABCD.EFGH dengan panjang rusuk 2. Jika P titik tengah HG, Q titik tengah FG, R titik tengah PQ, dan BS
adalah proyeksi BR pada bidang ABCD, maka panjang BS adalah .....
Nomor 17. Soal SPMB Mat IPA 2004
Diketahui kubus ABCD.EFGH dengan panjang rusuk $ a $ . P dan Q masing - masing merupakan titik tengah AB dan CD,
sedangkan R merupakan titik perpotongan EG dan FH. Jarak titik R ke bidang EPQH adalah ....
Nomor 18. Soal SPMB Mat IPA 2003
Diketahui kubus ABCD.EFGH dengan panjang rusuknya $ 2 a $ . Jika P titik tengah BF dan Q titik tengah EH, maka panjang PQ = ....
Nomor 19. Soal SPMB Mat IPA 2002
Bidang V dan W berpotongan tegak lurus sepanjang garis $ g $. Garis $ l $ membentuk sudut $ 45^\circ $ dengan V dan $ 30^\circ $
dengan W. Sinus sudut antara $ l $ dan $ g $ adalah .....
Nomor 20. Soal UMPTN Mat IPA 2001
Panjang rusuk kubus ABCD.EFGH adalah $ a $ . Jarak A ke diagonal BH adalah ....
Nomor 21. Soal UMPTN Mat IPA 2000
Dalam kubus ABCD.EFGH titik S adalah titik tengah sisi CD dan P adalah titik tengah diagonal ruang BH. Perbandingan
antara volume limas P.BCS dan volume kubus ABCD.EFGH adalah .....
Nomor 22. Soal Simak UI Mat IPA 2014
Diberikan kubus PQRS.TUVW. Titik A terletak di tengah rusuk VW dan titik B terletak di rusuk RV sedemikian sehingga VB=2BR. Titik C terletak di
perpanjangan rusuk UV sedemikian sehingga UV=2VC. Bidang $\Omega$ melalui A, B, dan C. Jika $\alpha$ adalah sudut terkecil yang terbentuk antara bidang
$\Omega$ dan perpanjangan rusuk QU, maka $ \tan 2\alpha =...$
Nomor 23. Soal SBMTPN Mat IPA 2014 Kode 523
Diberikan balok ABCD.EFGH dengan AB = AE = 4 dan BC = 3. Titik P dan Q masing-masing titik tengah FG dan GH. Maka tangen sudut bidang
diagonal FHDB dan bidang PQDB adalah ....
Nomor 24. Soal SBMTPN Mat IPA 2014 Kode 532
Diberikan kubus ABCD.EFGH dengan panjang rusuk $ 3p . \, $ Titik-titik P, Q, dan R masing-masing pada FB, FG, dan AD
sehingga BP = GQ = DR = $ p \, $ . Jika S adalah titik potong bidang yang melalui P, Q, dan R dengan rusuk DH, maka jarak
dari S ke P adalah .....
Nomor 25. Soal SBMTPN Mat IPA 2014 Kode 586
Diberitahukan kubus ABCD.EFGH dengan panjang rusuk $ 3p , \, $ titik-titik P, Q, dan R masing-masing pada FB, FG, dan AD
sehingga BP = GQ = DR = $ p . \, $ Jika $ \beta \, $ adalah irisan bidang yang melalui P, Q, dan R, maka tangen sudut
antara bidang $ \beta \, $ dan bidang alas adalah ....
Nomor 26. Soal SBMTPN Mat IPA 2014 Kode 542
Diketahui kubus ABCD.EFGH dengan panjang rusuk $ 2p . \, $ Titik-titik P, Q, dan R masing-masing adalah titik tengah FB, FG, dan AD.
Luas penampang irisan bidang yang melalui P, Q, dan R dan kubus ABCD.EFGH adalah .....
Nomor 27. Soal SPMK UB Mat IPA 2010
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Misalkan P adalah titik potong diagonal ABCD dan Q adalah
proyeksi B pada PF. Panjang PQ adalah ......
Nomor 28. Soal UTUL UGM Mat IPA 2013
Panjang rusuk kubus PQRS.TUVW adalah 6 cm. Titik X pada TW, Y pada UV, dan Z pada QR. Jika |TX| : |XW| = 1 : 2,
|UY| : |YV| = 2 : 1, dan PXYZ membentuk bidang datar, maka volume bangun TUYX.PQZ adalah ....
Nomor 29. Soal UTUL UGM Mat IPA 2013
Diketahui limas beraturan T.ABCD dengan alas berbentuk persegi dan tinggi limas $ 2\sqrt{3} \, $ cm. Jika $ T^\prime \, $ proyeksi T
pada bidang alas dan titik P adalah perpotongan garis berat segitiga TBC, maka panjang sisi alas limas agar $ T^\prime P \, $ tegak lurus
segitiga TBC adalah .....
Nomor 30. Soal SBMPTN Mat IPA 2015 Kode 517
Pada kubus ABCD.EFGH dengan panjang rusuk 4, titik P terletak pada segmen AF sehingga PF = 2AP. Titik Q adalah titik potong garis
GP dan bidang ABCD. Jika $ \alpha \, $ adalah sudut yang terbentuk antara garis GQ dan garis DA, maka nilai $ \cos \alpha \, $ adalah ....
Nomor 31. Soal UTUL UGM Mat IPA 2015 
Diketahui kubus ABCD.EFGH dengan panjang rusuk $ 4p \, $ . Titik P, Q, dan R berturut-turut terletak pada rusuk FG, BF, dan GH
dengan $ GP = BQ = GR = p . \, $ Sudut antara bidang yang melalui P, Q, R dan bidang ABCD adalah $ \alpha \, $ .
Nilai $ \tan \alpha \, $ adalah ....
Nomor 31. Soal UTUL UGM Mat IPA 2016 Kode 581
Limas segiempat beraturan T.ABCD mempunyai tinggi sama dengan dua kali panjang sisi ABCD. Jika titik E berada pada garis BC
dengan BE:EC=1:1 dan titik F berada pada garis TE dengan TF:FE=1:3, maka panjang proyeksi FE pada ABCD adalah .... kali sisi ABCD.
A). $ \frac{9}{8} \, $ B). $ \frac{5}{8} \, $ C). $ \frac{4}{8} \, $ D). $ \frac{3}{8} \, $ E). $ \frac{1}{8} $
Nomor 32. Soal UTUL UGM Mat IPA 2016 Kode 381 A). $ \frac{9}{8} \, $ B). $ \frac{5}{8} \, $ C). $ \frac{4}{8} \, $ D). $ \frac{3}{8} \, $ E). $ \frac{1}{8} $
Diketahui T.ABCD merupakan limas beraturan dengan alas bujur sangkar. Titik E pada TA
dengan $ TE:EA = 2 : 3 $ , titik F pada TB dengan $ TF:FB = 7:3$. Jika bidang yang melalui
EF dan sejajar BC memotong TC dan TD berturut-turut di G dan H, maka $ EH : FG = .... $
A). $ \frac{9}{8} \, $ B). $ \frac{5}{8} \, $ C). $ \frac{4}{8} \, $ D). $ \frac{3}{8} \, $ E). $ \frac{1}{8} $
Nomor 33. Soal SBMPTN Mat IPA 2016 Kode 245 A). $ \frac{9}{8} \, $ B). $ \frac{5}{8} \, $ C). $ \frac{4}{8} \, $ D). $ \frac{3}{8} \, $ E). $ \frac{1}{8} $
Diketahui kubus ABCD.EFGH dengan P merupakan titik tengah BF, dan Q
merupakan titik tengah DC. Jika $\angle PHQ = \theta$, maka
$ \cos \theta = .... $
A). $ \frac{2}{15}\sqrt{5} \, $ B). $ \frac{4}{15}\sqrt{5} \, $ C). $ \frac{2}{5}\sqrt{5} \, $ D). $ \frac{9}{130}\sqrt{65} \, $ E). $ \frac{4}{15}\sqrt{65} \, $
Nomor 34. Soal SBMPTN Mat IPA 2016 Kode 246 A). $ \frac{2}{15}\sqrt{5} \, $ B). $ \frac{4}{15}\sqrt{5} \, $ C). $ \frac{2}{5}\sqrt{5} \, $ D). $ \frac{9}{130}\sqrt{65} \, $ E). $ \frac{4}{15}\sqrt{65} \, $
Diketahui kubus ABCD.EFGH, titik P adalah titik potong diagonal AH dan DE,
titik Q adalah titik potong diagonal BG dan CF. Nilai $ \sin \angle BPQ $
adalah ....
A). $ \frac{\sqrt{3}}{3} \, $ B). $ \frac{\sqrt{3}}{2} \, $ C). $ \frac{\sqrt{3}}{6} \, $ D). $ \frac{\sqrt{3}}{4} \, $ E). $ \frac{\sqrt{2}}{2} \, $
Nomor 35. Soal SBMPTN Mat IPA 2016 Kode 247 A). $ \frac{\sqrt{3}}{3} \, $ B). $ \frac{\sqrt{3}}{2} \, $ C). $ \frac{\sqrt{3}}{6} \, $ D). $ \frac{\sqrt{3}}{4} \, $ E). $ \frac{\sqrt{2}}{2} \, $
Pada kubus ABCD.EFGH, titik M terletak pada diagonal BE dengan perbandingan
$ EM:MB = 1:3 $ dan N adalah titik tengah rusuk CD. Jika R terletak pada rusuk
AB dimana RM sejajar AE, maka $ \sin \angle MNR \, $ adalah .....
A). $ \frac{\sqrt{17}}{\sqrt{26}} \, $ B). $ \frac{2}{\sqrt{26}} \, $ C). $ \frac{3}{\sqrt{26}} \, $ D). $ \frac{\sqrt{5}}{\sqrt{17}} \, $ E). $ \frac{5}{\sqrt{17}} \, $
Nomor 36. Soal SBMPTN Mat IPA 2016 Kode 248 A). $ \frac{\sqrt{17}}{\sqrt{26}} \, $ B). $ \frac{2}{\sqrt{26}} \, $ C). $ \frac{3}{\sqrt{26}} \, $ D). $ \frac{\sqrt{5}}{\sqrt{17}} \, $ E). $ \frac{5}{\sqrt{17}} \, $
Diketahui kubus ABCD.EFGH, Titik M berada di rusuk AD sedemikian sehingga $ AM : MD = 1 : 2 $. Titik N berada di rusuk CD
sedemikian sehingga $ CN : ND = 1 : 2 $ . Titik P berada di rusuk DH sedemikian sehingga $ DP : PH = 2 : 1 $.
Jika $ \alpha $ adalah sudut antara bidang MNP dan garis PB, maka nilai $ \cos \alpha = .... $
A). $ \frac{5}{44} \sqrt{44} \, $ B). $ \frac{5}{33} \sqrt{33} \, $ C). $ \frac{5}{22} \sqrt{22} \, $ D). $ \frac{1}{13} \sqrt{13} \, $ E). $ \frac{1}{11} \sqrt{11} \, $
Nomor 37. Soal SBMPTN Mat IPA 2016 Kode 249 A). $ \frac{5}{44} \sqrt{44} \, $ B). $ \frac{5}{33} \sqrt{33} \, $ C). $ \frac{5}{22} \sqrt{22} \, $ D). $ \frac{1}{13} \sqrt{13} \, $ E). $ \frac{1}{11} \sqrt{11} \, $
Diketahui kubus ABCD.EFGH dengan rusuk 2 satuan. Titik K adalah titik tengah CD. Jika $ \alpha $ adalah sudut antara
AK dan BH, maka $ \cos \alpha = .... $
A). $ \frac{1}{3}\sqrt{3} \, $ B). $ \frac{1}{5}\sqrt{5} \, $ C). $ \frac{1}{15}\sqrt{15} \, $ D). $ \frac{1}{5}\sqrt{15} \, $ E). $ \frac{1}{3}\sqrt{15} \, $
Nomor 38. Soal SBMPTN Mat IPA 2016 Kode 250 A). $ \frac{1}{3}\sqrt{3} \, $ B). $ \frac{1}{5}\sqrt{5} \, $ C). $ \frac{1}{15}\sqrt{15} \, $ D). $ \frac{1}{5}\sqrt{15} \, $ E). $ \frac{1}{3}\sqrt{15} \, $
Diketahui kubus ABCD.EFGH, Titik M berada di rusuk AD sedemikian sehingga $ AM : MD = 1 : 2 $. Titik N berada di rusuk CD
sedemikian sehingga $ CN : ND = 1 : 2 $ . Titik P berada di rusuk DH sedemikian sehingga $ DP : PH = 2 : 1 $.
Jika $ \alpha $ adalah sudut antara bidang MNP dan bidang ACGE, maka nilai $ \sin \alpha = .... $
A). $ \frac{1}{3} \sqrt{6} \, $ B). $ \frac{1}{3} \sqrt{5} \, $ C). $ \frac{1}{3} \sqrt{4} \, $ D). $ \frac{1}{3} \sqrt{3} \, $ E). $ \frac{1}{3} \sqrt{2} \, $
Nomor 39. Soal SBMPTN Mat IPA 2016 Kode 251 A). $ \frac{1}{3} \sqrt{6} \, $ B). $ \frac{1}{3} \sqrt{5} \, $ C). $ \frac{1}{3} \sqrt{4} \, $ D). $ \frac{1}{3} \sqrt{3} \, $ E). $ \frac{1}{3} \sqrt{2} \, $
Pada kubus ABCD.EFGH, titik M terletak pada diagonal BE dengan perbandingan
$ EM:MB = 2:3 $ dan N adalah titik tengah rusuk CD. Jika R terletak pada rusuk
AB dimana RM sejajar AE, maka $ \cos \angle NMR \, $ adalah .....
A). $ \frac{6}{\sqrt{101}} \, $ B). $ \sqrt{\frac{101}{137}} \, $ C). $ \sqrt{\frac{6}{137}} \, $ D). $ \frac{3}{\sqrt{101}} \, $ E). $ \frac{3}{\sqrt{137}} \, $
Nomor 40. Soal SBMPTN Mat IPA 2016 Kode 252 A). $ \frac{6}{\sqrt{101}} \, $ B). $ \sqrt{\frac{101}{137}} \, $ C). $ \sqrt{\frac{6}{137}} \, $ D). $ \frac{3}{\sqrt{101}} \, $ E). $ \frac{3}{\sqrt{137}} \, $
Diketahui kubus ABCD.EFGH, Titik M berada di rusuk AD sedemikian sehingga $ AM : MD = 1 : 2 $. Titik N berada di rusuk CD
sedemikian sehingga $ CN : ND = 1 : 2 $ . Titik P berada di rusuk DH sedemikian sehingga $ DP : PH = 2 : 1 $.
Jika $ \alpha $ adalah sudut antara bidang MNP dan garis FH, maka nilai $ \sin \alpha = .... $
A). $ \frac{1}{3} \sqrt{6} \, $ B). $ \frac{1}{3} \sqrt{5} \, $ C). $ \frac{1}{3} \sqrt{4} \, $ D). $ \frac{1}{3} \sqrt{3} \, $ E). $ \frac{1}{3} \sqrt{2} \, $
Nomor 41. Soal UTUL UGM Mat IPA 2010 A). $ \frac{1}{3} \sqrt{6} \, $ B). $ \frac{1}{3} \sqrt{5} \, $ C). $ \frac{1}{3} \sqrt{4} \, $ D). $ \frac{1}{3} \sqrt{3} \, $ E). $ \frac{1}{3} \sqrt{2} \, $
Diketahui kubus ABCD.EFGH, dengan panjang rusuk $ a $, titik P pada perpanjangan DH sehingga $ DP = 2DH $.
Jarak titik F ke bidang PAC adalah ....
A). $ \frac{2a}{3} \, $ B). $ \frac{1}{2}a\sqrt{2} \, $ C). $ \frac{1}{2}a\sqrt{3} \, $ D). $ a \, $ E). $ \frac{3a}{2} \, $
Nomor 42. Soal SBMPTN MatDas 2017 Kode 224 A). $ \frac{2a}{3} \, $ B). $ \frac{1}{2}a\sqrt{2} \, $ C). $ \frac{1}{2}a\sqrt{3} \, $ D). $ a \, $ E). $ \frac{3a}{2} \, $

Diketahui kubus ABCD.EFGH dengan titik X terletak pada rusuk EF sejauh 2 cm dari F dan Y adalah titik potong perpanjangan AX dan perpanjangan BF. Jika panjang rusuk kubus tersebut 6 cm, maka jarak Y ke G adalah .... cm.
A). $ 2\sqrt{6} \, $ B). $ 3\sqrt{3} \, $ C). $ 3\sqrt{5} \, $ D). $ 2\sqrt{17} \, $ E). $ 3\sqrt{13} $

Diketahui kubus ABCD.EFGH dengan P adalah titik tengah BF dan Q adalah titik potong AP dan BE seperti pada gambar. Jika rusuk kubus tersebut adalah 6 cm, maka jarak Q ke H adalah .... cm
A). $ 3\sqrt{13} \, $ B). $ 2\sqrt{17} \, $ C). $ 3\sqrt{3} \, $ D). $ 2\sqrt{6} \, $ E). $ 4 \, $
Diketahui kubus ABCD.EFGH dengan P adalah titik tengah CG dan Q adalah titik
tengah AP, seperti pada gambar. Jika panjang rusuk kubus tersebut adalah 6 cm,
maka jarak Q ke H adalah .... cm
Nomor 45. Soal UTUL UGM Mat IPA 2017 Kode 713
Diketahui kubus ABCD.EFGH. Jika $ \alpha $ adalah sudut antara bidang AHF dan CHF, maka
$ \sin \alpha = .... $
A). $ -\frac{2}{3}\sqrt{2} \, $ B). $ -\frac{1}{3}\sqrt{2} \, $ C). $ \frac{1}{3} \, $ D). $ \frac{1}{3}\sqrt{2} \, $ E). $ \frac{2}{3}\sqrt{2} $
Nomor 46. Soal SBMPTN MatDas 2017 Kode 207 A). $ -\frac{2}{3}\sqrt{2} \, $ B). $ -\frac{1}{3}\sqrt{2} \, $ C). $ \frac{1}{3} \, $ D). $ \frac{1}{3}\sqrt{2} \, $ E). $ \frac{2}{3}\sqrt{2} $

Diketahui kubus ABCD.EFGH dengan M dan N berturut-turut adalah titik tengah FG dan BC, serta T adalah titik pada AM sehingga NT tegak lurus AM seperti pada gambar. Jika panjang rusuk kubus tersebut 8 cm, maka panjang NT adalah ... cm.
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Jarak titik C ke bidang
BDG adalah ....
A). $ \frac{4}{3}\sqrt{3} \, $ B). $ \frac{3}{4}\sqrt{3} \, $ C). $ \frac{4}{3}\sqrt{2} \, $ D). $ \frac{3}{4}\sqrt{2} \, $ E). $ \frac{8}{3} $
Update bulan November 2017 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya. A). $ \frac{4}{3}\sqrt{3} \, $ B). $ \frac{3}{4}\sqrt{3} \, $ C). $ \frac{4}{3}\sqrt{2} \, $ D). $ \frac{3}{4}\sqrt{2} \, $ E). $ \frac{8}{3} $
Nomor 48. Soal UM Undip 2016 Mat dasar IPA
Diketahui kubus ABCD.EFGH dengan panjang rusuk $ a $, P dan Q masing-masing titik tengah
HG dan EH. Sedangkan R titik tengah PQ. Jika BT adalah proyeksi BR pada bidang ABCD,
maka jarak T dengan bidang QBP adalah ....
A). $ \frac{4a}{17}\sqrt{17} \, $ B). $ \frac{3a}{17}\sqrt{17} \, $ C). $ \frac{2a}{17}\sqrt{17} \, $ D). $ \frac{3a}{13}\sqrt{13}\, $ E). $ \frac{a}{7}\sqrt{7} $
Nomor 49. Soal UM UGM 2009 Mat IPA A). $ \frac{4a}{17}\sqrt{17} \, $ B). $ \frac{3a}{17}\sqrt{17} \, $ C). $ \frac{2a}{17}\sqrt{17} \, $ D). $ \frac{3a}{13}\sqrt{13}\, $ E). $ \frac{a}{7}\sqrt{7} $
Diketahui limas segi empat beraturan T.ABCD dengan panjang rusuk AB adalah $ a $. Jika
$ \alpha $ adalah sudut antara bidang TAB dan ABCD dengan $ \sin \alpha = \frac{3}{5} $ ,
maka panjang rusuk TA adalah ....
A). $ \frac{a}{8}\sqrt{44} \, $ B). $ \frac{a}{8}\sqrt{42} \, $ C). $ \frac{a}{10}\sqrt{41} \, $ D). $ \frac{a}{9}\sqrt{41} \, $ E). $ \frac{a}{8}\sqrt{41} $
Nomor 50. Soal UM UGM 2008 Mat IPA A). $ \frac{a}{8}\sqrt{44} \, $ B). $ \frac{a}{8}\sqrt{42} \, $ C). $ \frac{a}{10}\sqrt{41} \, $ D). $ \frac{a}{9}\sqrt{41} \, $ E). $ \frac{a}{8}\sqrt{41} $
Pada kubus ABCD.EFGH, P pada EG sehingga $ EP = 3PG $. Jika jarak E ke AP adalah $ a $,
maka rusuk kubus tersebut adalah ....
A). $ \frac{a}{3}\sqrt{15} \, $ B). $ \frac{4a}{3} \, $ C). $ \frac{a}{3}\sqrt{17} \, $ D). $ a\sqrt{2} \, $ E). $ \frac{a}{2}\sqrt{5} $
Nomor 51. Soal UM UGM 2007 Mat IPA A). $ \frac{a}{3}\sqrt{15} \, $ B). $ \frac{4a}{3} \, $ C). $ \frac{a}{3}\sqrt{17} \, $ D). $ a\sqrt{2} \, $ E). $ \frac{a}{2}\sqrt{5} $
Alas bidang empat D.ABC berbentuk segitiga siku-siku dama kaki dengan
$ \angle BAC = 90^\circ $. Proyeksi D pada segitiga ABC adalah E sehingga E merupakan
titik tengah BC. Jika $ AB = AC = p $ dan $ DE = 2p $ , maka $ AD = .... $
A). $ \frac{3}{2}p\sqrt{2} \, $ B). $ \frac{3}{2}p\sqrt{3} \, $ C). $ 3p \, $ D). $ p\sqrt{6} \, $ E). $ p\sqrt{5} $
Nomor 52. Soal UM UGM 2006 Mat IPA A). $ \frac{3}{2}p\sqrt{2} \, $ B). $ \frac{3}{2}p\sqrt{3} \, $ C). $ 3p \, $ D). $ p\sqrt{6} \, $ E). $ p\sqrt{5} $
Diketahui kubus ABCD.EFGH dengan panjang rusuk 4 cm. Titik P pada rusuk AE dengan $ AP = 3 \, $
cm, Q titik tengah AB. Luas segitiga HPQ adalah ....
A). $ \frac{1}{2}\sqrt{53} \, $ cm$^2 $
B). $ \sqrt{53} \, $ cm$^2 $
C). $ 2\sqrt{53} \, $ cm$^2 $
D). $ \frac{1}{3}\sqrt{53} \, $ cm$^2 $
E). $ \frac{2}{3}\sqrt{53} \, $ cm$^2 $
Nomor 53. Soal UM UGM 2005 Mat IPA A). $ \frac{1}{2}\sqrt{53} \, $ cm$^2 $
B). $ \sqrt{53} \, $ cm$^2 $
C). $ 2\sqrt{53} \, $ cm$^2 $
D). $ \frac{1}{3}\sqrt{53} \, $ cm$^2 $
E). $ \frac{2}{3}\sqrt{53} \, $ cm$^2 $
DIketahui limas segiempat T.ABCD dengan rusuk-rusuk tegak 15 cm, bidang alasnya ABCD
berbentuk persegi panjang dengan AB = 10 cm dan BC = 12 cm. Jika $ \alpha $ adalah
sudut antara bidang TAB dengan bidang alas ABCD, maka $ \sin \alpha = .... $
A). $ \frac{2}{5}\sqrt{19} \, $ cm
B). $ \frac{1}{10}\sqrt{78} \, $ cm
C). $ \frac{4}{5}\sqrt{5} \, $ cm
D). $ \frac{1}{10}\sqrt{82} \, $ cm
E). $ \frac{2}{5}\sqrt{21} \, $ cm
Nomor 54. Soal UM UGM 2005 Mat IPA Kode 612 A). $ \frac{2}{5}\sqrt{19} \, $ cm
B). $ \frac{1}{10}\sqrt{78} \, $ cm
C). $ \frac{4}{5}\sqrt{5} \, $ cm
D). $ \frac{1}{10}\sqrt{82} \, $ cm
E). $ \frac{2}{5}\sqrt{21} \, $ cm
DIketahui kubus ABCD.EFGH dengan rusuk $ a $. P adalah titik pada perpanjangan AE sehingga
$ PE = \frac{1}{2}a $. Jika bidang PBD memotong bidang atas EFGH sepanjang QR,
maka $ QR = .... $
A). $ \frac{1}{3}a \, $ B). $ \frac{1}{2}a \, $ C). $ \frac{1}{3}a\sqrt{2} \, $
D). $ \frac{1}{2}a\sqrt{2} \, $ E). $ \frac{2}{3}a\sqrt{2} \, $
Nomor 55. Soal UM UGM 2004 Mat IPA A). $ \frac{1}{3}a \, $ B). $ \frac{1}{2}a \, $ C). $ \frac{1}{3}a\sqrt{2} \, $
D). $ \frac{1}{2}a\sqrt{2} \, $ E). $ \frac{2}{3}a\sqrt{2} \, $
Pada kubus ABCD.EFGH, titik P pada AE dengan 3AP = PE, dan $ \alpha $ adalah sudut
antara PH dan BC. Nilai $ \sin \alpha $ adalah ....
A). $ \frac{2}{\sqrt{10}} \, $ B). $ \frac{4}{\sqrt{41}} \, $ C). $ \frac{2}{3} \, $ D). $ \frac{3}{4} \, $ E). $ \frac{3}{5} \, $
Nomor 56. Soal UM UGM 2003 Mat IPA A). $ \frac{2}{\sqrt{10}} \, $ B). $ \frac{4}{\sqrt{41}} \, $ C). $ \frac{2}{3} \, $ D). $ \frac{3}{4} \, $ E). $ \frac{3}{5} \, $
Diketahui limas segitiga P.ABC. Titik K, L, M berturut-turut adalah titik tengah-titik
tengah PA, PB, PC. Dibuat bidang pengiris KLM dan bidang pengiris KBM.
Jika :
$ \, \, \, V_1 = \, $ volume bidang empat B.KLM,
$ \, \, \, V_2 = \, $ volume limas terpancung ABC.KLM,
maka $ \frac{V_2}{V_1} = .... $
A). $ 8 \, $ B). $ 7 \, $ C). $ 6 \, $ D). $ 4 \, $ E). $ 2 \, $
Nomor 57. Soal UM UNDIP 2017 Mat IPA $ \, \, \, V_1 = \, $ volume bidang empat B.KLM,
$ \, \, \, V_2 = \, $ volume limas terpancung ABC.KLM,
maka $ \frac{V_2}{V_1} = .... $
A). $ 8 \, $ B). $ 7 \, $ C). $ 6 \, $ D). $ 4 \, $ E). $ 2 \, $
DIketahui kubus ABCD.EFGH dengan panjang rusuk $ a $ cm. Titik P terletak pada diagonal AC,
dengan perbandingan $ AP : PC = 3 : 1 $. Maka jarak titik P pada bidang BDG
sama dengan ....
A). $ \frac{a}{6}\sqrt{3} \, $ B). $ \frac{a}{6}\sqrt{2} \, $ C). $ \frac{a}{3}\sqrt{3} \, $ D). $ \frac{a}{3}\sqrt{2} \, $ E). $ \frac{a}{6}\sqrt{6} \, $
A). $ \frac{a}{6}\sqrt{3} \, $ B). $ \frac{a}{6}\sqrt{2} \, $ C). $ \frac{a}{3}\sqrt{3} \, $ D). $ \frac{a}{3}\sqrt{2} \, $ E). $ \frac{a}{6}\sqrt{6} \, $
Update bulan Desember 2018 "kumpulan soal-soal Matematika Seleksi Masuk PTN" dilengkapi dengan pembahasannya.
Nomor 58. Soal SBMPTN 2017 MatDas Kode 226
Diketahui kubus ABCD.EFGH dengan P dan Q berturut-turut adalah titik tengah HG dan
BC. Jika panjang rusuk kubus tersebut 4 cm, maka jarak P ke Q adalah ... cm.
A). $ 2\sqrt{3} \, $ B). $ 2\sqrt{6} \, $ C). $ 6\sqrt{2} \, $ D). $ 6\sqrt{3} \, $ E). $ 6\sqrt{6} $
Nomor 59. Soal SBMPTN 2017 MatDas Kode 202 A). $ 2\sqrt{3} \, $ B). $ 2\sqrt{6} \, $ C). $ 6\sqrt{2} \, $ D). $ 6\sqrt{3} \, $ E). $ 6\sqrt{6} $
Diketahui kubus ABCD.EFGH dengan P adalah titik potong diagonal bidang EFGH dan V
adalah titik potong perpanjangan CG dengan perpanjangan AP, seperti pada gambar.
Jika panjang rusuk kubus tersebut 6 cm, maka panjang AV adalah ... cm.
A). $ 6\sqrt{6} \, $ B). $ 7\sqrt{3} \, $ C). $ 8\sqrt{2} \, $ D). $ 3\sqrt{13} \, $ E). $ 2\sqrt{17} $
Nomor 60. Soal SBMPTN 2017 MatDas Kode 213 A). $ 6\sqrt{6} \, $ B). $ 7\sqrt{3} \, $ C). $ 8\sqrt{2} \, $ D). $ 3\sqrt{13} \, $ E). $ 2\sqrt{17} $
Diketahui kubus ABCD.EFGH dengan T adalah titik tengah EF dan U titik tengah BC. Jika
panjang rusuk kubus tersebut adalah 6 cm, maka panjang TU adalah .... cm.
A). $ 3\sqrt{6} \, $ B). $ 5\sqrt{2} \, $ C). $ 4\sqrt{3} \, $ D). $ 3\sqrt{5} \, $ E). $ 2\sqrt{7} $
Nomor 61. Soal SBMPTN 2017 MatDas Kode 222 A). $ 3\sqrt{6} \, $ B). $ 5\sqrt{2} \, $ C). $ 4\sqrt{3} \, $ D). $ 3\sqrt{5} \, $ E). $ 2\sqrt{7} $
Diketahui kubus ABCD.EFGH dengan P adalah titik tengah HG dan Q adalah titik tengah BC.
Jika jarak P ke Q adalah 6 cm, maka panjang rusuk kubus tersebut adalah .... cm.
A). $ \sqrt{6} \, $ B). $ \frac{3}{2}\sqrt{6} \, $ C). $ 2\sqrt{6} \, $ D). $ \frac{5}{2}\sqrt{6} \, $ E). $ 3\sqrt{6} $
Nomor 62. Soal SBMPTN 2017 MatDas Kode 232 A). $ \sqrt{6} \, $ B). $ \frac{3}{2}\sqrt{6} \, $ C). $ 2\sqrt{6} \, $ D). $ \frac{5}{2}\sqrt{6} \, $ E). $ 3\sqrt{6} $
Diketahui kubus ABCD.EFGH dengan titik P terletak pada perpanjangan BF sehingga FP = 3 cm
dan garis AP berpotongan dengan garis EF di titik Q. Jika panjang rusuk kubus tersebut
adalah 6 cm, maka jarak Q ke D adalah ..... cm.
A). $ 2\sqrt{13} \, $ B). $ 2\sqrt{18} \, $ C). $ 2\sqrt{22} \, $ D). $ 4\sqrt{7} \, $ E). $ 4\sqrt{11} $
Nomor 63. Soal SBMPTN 2018 Matipa Kode 452 A). $ 2\sqrt{13} \, $ B). $ 2\sqrt{18} \, $ C). $ 2\sqrt{22} \, $ D). $ 4\sqrt{7} \, $ E). $ 4\sqrt{11} $
Diketahui kubus ABCD.EFGH dengan panjang rusuk $ 2\sqrt{2} $ cm. Jika titik P di
tengah-tengah AB dan titik Q di tengah-tengah BC, maka jarak antara titik H dengan
garis PQ adalah ..... cm.
A). $ \sqrt{15} \, $ B). $ 4 \, $ C). $ \sqrt{17} \, $ D). $ 3\sqrt{2} \, $ E). $ \sqrt{19} $
Nomor 64. Soal UM UNDIP 2018 Matipa A). $ \sqrt{15} \, $ B). $ 4 \, $ C). $ \sqrt{17} \, $ D). $ 3\sqrt{2} \, $ E). $ \sqrt{19} $
Diketahui kubus ABCD.EFGH dengan panjang rusuk $ a $ cm. Titik Q dan R masing-masing adalah
titik tengah CD dan CB. Jika T adalah perpotongan QR dan AC, dan S adalah proyeksi T pada
bidang AFH, maka panjang AS sama dengan ...
A). $ \frac{a}{8}\sqrt{6} \, $ B). $ \frac{a}{4}\sqrt{3} \, $ C). $ \frac{a}{3}\sqrt{6} \, $ D). $ \frac{a}{2}\sqrt{3} \, $ E). $ \frac{a}{2}\sqrt{6} $
A). $ \frac{a}{8}\sqrt{6} \, $ B). $ \frac{a}{4}\sqrt{3} \, $ C). $ \frac{a}{3}\sqrt{6} \, $ D). $ \frac{a}{2}\sqrt{3} \, $ E). $ \frac{a}{2}\sqrt{6} $
Untuk kumpulan soal utbk 2019 matematika saintek dan matematika soshum, silahkan kunjungi link berikut:
Kumpulan Soal UTBK 2019 Matematika Saintek
Kumpulan Soal UTBK 2019 Matematika Soshum




