Blog KoMa - Pada artikel ini kita akan membahas materi Ringkasan Fungsi Kuadrat Pertama Soshum - umptn beserta
soal-soal yang terkait yang khususnya tentang soal-soal UMPTN baik seleksi bersama ataupun seleksi mandiri seperti SPMB, SNMPTN, SBMPTN, UTBK,
UM UGM (utul), simak UI, UM UNDIP, UNPAD, dan lainnya. Untuk melengkapkan materi dan memudahkan pemahaman, kami juga sertakan beberapa contoh soal
pendukung (bila diperlukan) untuk menguasai materi Fungsi Kuadrat Pertama ini. Untuk soal-soal Fungsi Kuadrat kita bagi menjadi dua
bagian yaitu contoh soal dan soal latihan mandiri. Untuk soal latihan mandiri, teman-teman bisa mencobanya terlebih dahulu, setelah itu baru cek solusinya
dibagian bawahnya untuk masing-masing soal latihan mandiri. Kami yakin, dengan tekun belajar maka materi Ringkasan Fungsi Kuadrat Pertama Soshum - umptn ini
bisa teman-teman kuasai dengan baik.
Untuk contoh detail tentang bentuk umum fungsi kuadrat, silahkan sahabat koma kunjungi link berikut:
Bentuk umum fungsi kuadrat
Contoh soal :
Dari fungsi kuadrat $ f(x) = 2x^2 - 4x + 5 $ , tentukan
a). Persamaan sumbu simetrinya
b). Nilai minimum fungsi
c). Titik balik/titik puncaknya
Penyelesaian :
$ f(x) = 2x^2 - 4x + 5 \rightarrow a = 2, \, b = -4, \, c = 5 $
a). Persamaan sumbu simetrinya : $ x = x_p $
$ x = \frac{-b}{2a} \rightarrow x = \frac{-(-4)}{2 \times 2} \rightarrow x = 1 $
Sehingga persamaan sumbu simetrinya yaitu $ x = 1 $
b). Nilai minimum fungsi
Nilai minimum $ = y_p $
$ y_p = \frac{D}{-4a} = \frac{b^2-4ac}{-4a} $
$ y_p = \frac{(-4)^2 - 4 \times 2 \times 5}{-4\times 2} = \frac{-24}{-8} = 3 $
atau $ y_p = f(x_p) = f(1) = 2 (1^2) - 4 \times 1 + 5 = 2 - 4 + 5 = 3 $
Sehingga nilai minimum fungsi = 3.
c). Titik balik/titik puncaknya $ (x_p, y_p) $
Pada bagian (a) dan (b) kita peroleh :
$ x_p = 1 \, $ dan $ y_p = 3 $
Sehingga titik puncaknya :
$ (x_p , y_p) = ( 1 , 3) $
Jenisnya minimum karena $ a > 0 $.
Contoh soal umptn :
1. Soal SBMPTN 2017 MatDas 224
Sumbu simetri grafik $ f(x) = ax^2 + bx + c $ adalah $ x = 1 $. Jika $ f(0)=0 $ dan $ f(4) = -16$ , maka nilai $ b - a $ adalah ....
A). $ 6 \, $
B). $ 5 \, $
C). $ 4 \, $
D). $ 3 \, $
E). $ 2 \, $
2. Soal Selma UM 2014 MatIpa
Diketahui $ \, f(x) = -2x^2 -(p+1)x + 2p. \, $ Fungsi $ f(x) \, $ mempunyai nilai maksimum 8. Jika $ p \, $ bernilai $ p_1 \, $ atau $ p_2 . \, $ Nilai $ p_1 + p_2 \, $ adalah ....
A). $ -16 $
B). $ -17 $
C). $ -18 $
D). $ -19 $
E). $ -20 $
Untuk contoh detail tentang sketsa dan menggambar grafik fungsi kuadrat, silahkan kunjungi link berikut:
Sketsa dan Menggambar grafik fungsi kuadrat
Contoh soal :
3). Gambarla grafik fungsi kuadrat berikut:
a). $ y = x^2 - 2x - 8 $
b). $ y = x^2 - 6x + 9 $
c). $ y = 2x^2 + x + 3 $
Untuk contoh soal yang lebih mendetail tentang teknik menggeser grafik fungsi kuadrat, silahkan kunjungi link berikut :
Teknik Menggeser Grafik
Contoh soal umptn :
4. Soal SBMPTN 2015 MatDas 617
Jika grafik parabola $ y = x^2 - 3x + a \, $ digeser ke kiri searah sumbu-x sejauh 2 satuan sehingga melalui titik (0,0), maka nilai $ a \, $ adalah ....
A). $ -2 $
B). $ -1 $
C). 0
D). 1
E). 2
5). Soal UTBK 2019 Soshum
jika kurva $ y = x^2 + 5x - 2p $ melalui titik $ (1,p) $ dan memotong sumbu X di $ (x_1, y_1) $ dan $ (x_2, y_2) $, maka nilai $ x_1^2 + y_1^2 + x_2^2 + y_2^2 = ... $
A). 31
B). 32
C). 33
D). 34
E). 35
6). Soal SBMPTN 2018 MatDas 552
Diketahui grafik fungsi $ f(x) = -x^2 + ax + b $ memotong sumbu X di titik $ (-p-3,0) $ dan titik $ (p,0) $ untuk suatu bilangan prima $ p $. Jika $ p + 3 $ juga merupakan suatu bilangan prima, maka nilai maksimum dari $ f(x) $ adalah ...
A). $ \frac{49}{2} \, $
B). $ \frac{49}{4} \, $
C). $ 10 \, $
D). $ -\frac{49}{4} \, $
E). $ -\frac{49}{2} $
7). Soal SBMPTN 2017 MatDas 213
Koordinat titik puncak grafik $ f(x) = ax^2 + bx + c $ adalah $ (4,2) $. Jika $ f(2) = 0 $, maka nilai $ 6a + b = ..... $
A). $ 5 \, $
B). $ 4 \, $
C). $ 3 \, $
D). $ 2 \, $
E). $ 1 $
8). Soal UM UGM 2016 MatDas 571
Diketahui ordinat titik puncak fungsi kuadrat $ f(x) = ax^2 + bx + c \, $ adalah 2. Jika $ f(2) = f(4) = 0 \, $ maka $ a + b + c = .... $
A). $-10 \, $
B). $ -6 \, $
C). $ -4 \, $
D). $ 4 \, $
E). $ 6 $
9). Soal SBMPTN 2015 MatDas 622
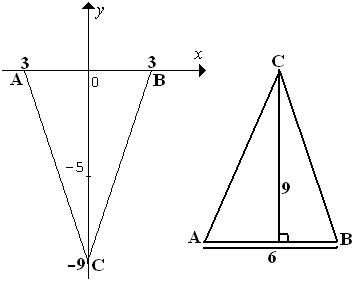
Jika grafik fungsi $ y = x^2 - 9 \, $ memotong sumbu x di titik A dan B, serta memotong sumbu y di titik C, maka luas segitiga ABC adalah ....
A). 36
B). 33
C). 30
D). 27
E). 24
Tentu, beberapa contoh soal di atas masih terasa kurang jika benar-benar ingin menguasai berbagai variasi soal-soal Fungsi Kuadrat seleksi PTN. Untuk lebih memaksimalkan belajarnya, silahkan sahabat koma kunjungi link berikut :
Kumpulan soal Fungsi Kuadrat seleksi PTN .
Demikian pembahasan materi Ringkasan Fungsi Kuadrat Pertama Soshum - umptn dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan UMPTN (Ujian Masuk Perguruan Tinggi Negeri) bidang Matematika pada link Daftar Materi UMPTN Bidang Matematika. Jika ada saran atau kritikan atau lainnya yang sifatnya membangaun, silahkan untuk tulis komen pada kolom komentar dibagian bawah setiap artikel. Semoga artikel ini bermanfaat. Terimakasih.
(A). Bentuk Umum Fungsi Kuadrat
Adapun bentuk umum fungsi kuadrat :
$ f(x) = ax^2 + bx + c $
Atau
$ y = ax^2 + bx + c $
dengan $ a, \, b, \, c \in R \, $ dan $ a \neq 0 $
$ f(x) = ax^2 + bx + c $
Atau
$ y = ax^2 + bx + c $
dengan $ a, \, b, \, c \in R \, $ dan $ a \neq 0 $
Keterangan :
$ x \, $ disebut variabel bebasnya
$ a \, $ adalah koefisien $ x^2 $
$ b \, $ adalah koefisien $ x $
$ c \, $ disebut konstanta
$ x \, $ disebut variabel bebasnya
$ a \, $ adalah koefisien $ x^2 $
$ b \, $ adalah koefisien $ x $
$ c \, $ disebut konstanta
Untuk contoh detail tentang bentuk umum fungsi kuadrat, silahkan sahabat koma kunjungi link berikut:
Bentuk umum fungsi kuadrat
(B). Karakteristik Grafik Fungsi Kuadrat
Perhatikan grafik fungsi kuadrat berikut :
Catatan :
-). Grafik fungsi kuadrat berbentuk parabola sehingga grafik fungsi kuadrat juga disebut parabola.
-). Setiap titik yang dilalui atau titik yang berada pada parabola, maka titik tersebut boleh disubstitusi ke fungsi parabola tersebut.
-). Mensubstitusi titik yang dilalui oleh sebuah grafik ke fungsinya berlaku untuk semua jenis fungsi (tidak hanya untuk fungsi kuadrat).
Catatan :
-). Grafik fungsi kuadrat berbentuk parabola sehingga grafik fungsi kuadrat juga disebut parabola.
-). Setiap titik yang dilalui atau titik yang berada pada parabola, maka titik tersebut boleh disubstitusi ke fungsi parabola tersebut.
-). Mensubstitusi titik yang dilalui oleh sebuah grafik ke fungsinya berlaku untuk semua jenis fungsi (tidak hanya untuk fungsi kuadrat).
Karakteristik grafik fungsi kuadrat :
-). Untuk bentuk $ y = ax^2 + bx + c $ , arah kurva ada dua yaitu :
terbuka keatas (senyum) saat $ a > 0 $
terbuka kebawah (cemberut) saat $ a < 0 $
-). Terdapat titik balik/titik puncak $ (x_p , y_p) $.
Rumus menentukan titik puncak yaitu :
$ x_p = \frac{-b}{2a} \, $
$ y_p = \frac{D}{-4a} \, $ atau $ y_p = f(x_p) \, $
dengan $ D = b^2 - 4ac $
-). Jenis-jenis titik baliknya :
titik balik maksimum saat $ a < 0 $
titik balik minimum saat $ a > 0 $
-). Persamaan sumbu simetri :
$ x = x_p \rightarrow x = \frac{-b}{2a} $
-). Nilai Optimum (maksimum atau minimum) fungsi kuadrat
Nilai maksimum atau minimum = $ y_p $
-). Untuk bentuk $ y = ax^2 + bx + c $ , arah kurva ada dua yaitu :
terbuka keatas (senyum) saat $ a > 0 $
terbuka kebawah (cemberut) saat $ a < 0 $
-). Terdapat titik balik/titik puncak $ (x_p , y_p) $.
Rumus menentukan titik puncak yaitu :
$ x_p = \frac{-b}{2a} \, $
$ y_p = \frac{D}{-4a} \, $ atau $ y_p = f(x_p) \, $
dengan $ D = b^2 - 4ac $
-). Jenis-jenis titik baliknya :
titik balik maksimum saat $ a < 0 $
titik balik minimum saat $ a > 0 $
-). Persamaan sumbu simetri :
$ x = x_p \rightarrow x = \frac{-b}{2a} $
-). Nilai Optimum (maksimum atau minimum) fungsi kuadrat
Nilai maksimum atau minimum = $ y_p $
Contoh soal :
Dari fungsi kuadrat $ f(x) = 2x^2 - 4x + 5 $ , tentukan
a). Persamaan sumbu simetrinya
b). Nilai minimum fungsi
c). Titik balik/titik puncaknya
Penyelesaian :
$ f(x) = 2x^2 - 4x + 5 \rightarrow a = 2, \, b = -4, \, c = 5 $
a). Persamaan sumbu simetrinya : $ x = x_p $
$ x = \frac{-b}{2a} \rightarrow x = \frac{-(-4)}{2 \times 2} \rightarrow x = 1 $
Sehingga persamaan sumbu simetrinya yaitu $ x = 1 $
b). Nilai minimum fungsi
Nilai minimum $ = y_p $
$ y_p = \frac{D}{-4a} = \frac{b^2-4ac}{-4a} $
$ y_p = \frac{(-4)^2 - 4 \times 2 \times 5}{-4\times 2} = \frac{-24}{-8} = 3 $
atau $ y_p = f(x_p) = f(1) = 2 (1^2) - 4 \times 1 + 5 = 2 - 4 + 5 = 3 $
Sehingga nilai minimum fungsi = 3.
c). Titik balik/titik puncaknya $ (x_p, y_p) $
Pada bagian (a) dan (b) kita peroleh :
$ x_p = 1 \, $ dan $ y_p = 3 $
Sehingga titik puncaknya :
$ (x_p , y_p) = ( 1 , 3) $
Jenisnya minimum karena $ a > 0 $.
Contoh soal umptn :
1. Soal SBMPTN 2017 MatDas 224
Sumbu simetri grafik $ f(x) = ax^2 + bx + c $ adalah $ x = 1 $. Jika $ f(0)=0 $ dan $ f(4) = -16$ , maka nilai $ b - a $ adalah ....
A). $ 6 \, $
B). $ 5 \, $
C). $ 4 \, $
D). $ 3 \, $
E). $ 2 \, $
2. Soal Selma UM 2014 MatIpa
Diketahui $ \, f(x) = -2x^2 -(p+1)x + 2p. \, $ Fungsi $ f(x) \, $ mempunyai nilai maksimum 8. Jika $ p \, $ bernilai $ p_1 \, $ atau $ p_2 . \, $ Nilai $ p_1 + p_2 \, $ adalah ....
A). $ -16 $
B). $ -17 $
C). $ -18 $
D). $ -19 $
E). $ -20 $
(C). Sketsa dan Menggambar Grafik Fungsi Kuadrat
Langkah-langkah menggambar grafik fungsi kuadrat :
1). Lihat nilai $ a $.
2). Menentukan titik potong (tipot) pada sumbu X (jika ada) dengan cara mensubstitusi $ y = 0 \, $ , sehingga diperoleh akar-akar dari $ ax^2+bx+c = 0 \, $ yaitu $ x_1 \, $ dan $ x_2 \, $ . Artinya tipotnya $ (x_1,0) \, $ dan $ (x_2,0) $ .
3). Menentukan titik potong (tipot) pada sumbu Y dengan cara mensubstitusi $ x = 0 \, $ , sehingga diperoleh $ y = c \, $ . Artinya tipotnya $ (0,c) $
4). Menentukan titik balik/puncak $ (x_p,y_p) $
Rumus : $ x_p = \frac{-b}{2a} \, $ dan $ y_p = \frac{D}{-4a} \, $ atau $ y_p = f(x_p)= f\left( \frac{-b}{2a} \right) $
Sehingga titik balik/puncaknya :
$ (x_p,y_p)= \left( \frac{-b}{2a} , \frac{D}{-4a} \right) \, $ atau $ (x_p,y_p)= \left( \frac{-b}{2a} , f\left( \frac{-b}{2a} \right) \right) $
5). Menentukan sembarang titik bantuan lainnya agar menggambar lebih mudah, dengan cara memilih beberapa nilai $ x \, $ dan disubstitusikan ke FK.
dengan $ D = b^2 - 4ac \, ( D \, $ disebut nilai Diskriminan seperti pada persamaan kuadrat).
1). Lihat nilai $ a $.
2). Menentukan titik potong (tipot) pada sumbu X (jika ada) dengan cara mensubstitusi $ y = 0 \, $ , sehingga diperoleh akar-akar dari $ ax^2+bx+c = 0 \, $ yaitu $ x_1 \, $ dan $ x_2 \, $ . Artinya tipotnya $ (x_1,0) \, $ dan $ (x_2,0) $ .
3). Menentukan titik potong (tipot) pada sumbu Y dengan cara mensubstitusi $ x = 0 \, $ , sehingga diperoleh $ y = c \, $ . Artinya tipotnya $ (0,c) $
4). Menentukan titik balik/puncak $ (x_p,y_p) $
Rumus : $ x_p = \frac{-b}{2a} \, $ dan $ y_p = \frac{D}{-4a} \, $ atau $ y_p = f(x_p)= f\left( \frac{-b}{2a} \right) $
Sehingga titik balik/puncaknya :
$ (x_p,y_p)= \left( \frac{-b}{2a} , \frac{D}{-4a} \right) \, $ atau $ (x_p,y_p)= \left( \frac{-b}{2a} , f\left( \frac{-b}{2a} \right) \right) $
5). Menentukan sembarang titik bantuan lainnya agar menggambar lebih mudah, dengan cara memilih beberapa nilai $ x \, $ dan disubstitusikan ke FK.
dengan $ D = b^2 - 4ac \, ( D \, $ disebut nilai Diskriminan seperti pada persamaan kuadrat).
Untuk contoh detail tentang sketsa dan menggambar grafik fungsi kuadrat, silahkan kunjungi link berikut:
Sketsa dan Menggambar grafik fungsi kuadrat
Contoh soal :
3). Gambarla grafik fungsi kuadrat berikut:
a). $ y = x^2 - 2x - 8 $
b). $ y = x^2 - 6x + 9 $
c). $ y = 2x^2 + x + 3 $
(C). Teknik Menggeser Grafik
Misalkan ada fungsi awal : $ y = f(x) $
Mengalami pergeseran menjadi : $ y = f(x \pm b) \pm c $
Artinya :
(a). digeser searah sumbu X sejauh $ b $ dengan :
untuk $ + b $ ke kiri
untuk $ - b $ ke kanan
(b). digeser searah sumbu Y sejauh $ c $ dengan :
untuk $ + c $ ke atas
untuk $ - c $ ke bawah
Catatan :
-). Untuk searah X (kanan atau kiri) tandanya berlawanan dari tanda pada sumbu X
-). Untuk searah Y (atas atau bawah) tandanya searah dari tanda pada sumbu Y
-). Teknik menggeser ini juga bisa menggunakan konsep pergeseran (Translasi) pada transformasi geometri karena pembuktian rumus di atas menggunakan konsep translasi.
-). Teknik menggeser ini berlaku umum untuk semua jenis fungsi.
Mengalami pergeseran menjadi : $ y = f(x \pm b) \pm c $
Artinya :
(a). digeser searah sumbu X sejauh $ b $ dengan :
untuk $ + b $ ke kiri
untuk $ - b $ ke kanan
(b). digeser searah sumbu Y sejauh $ c $ dengan :
untuk $ + c $ ke atas
untuk $ - c $ ke bawah
Catatan :
-). Untuk searah X (kanan atau kiri) tandanya berlawanan dari tanda pada sumbu X
-). Untuk searah Y (atas atau bawah) tandanya searah dari tanda pada sumbu Y
-). Teknik menggeser ini juga bisa menggunakan konsep pergeseran (Translasi) pada transformasi geometri karena pembuktian rumus di atas menggunakan konsep translasi.
-). Teknik menggeser ini berlaku umum untuk semua jenis fungsi.
Untuk contoh soal yang lebih mendetail tentang teknik menggeser grafik fungsi kuadrat, silahkan kunjungi link berikut :
Teknik Menggeser Grafik
Contoh soal umptn :
4. Soal SBMPTN 2015 MatDas 617
Jika grafik parabola $ y = x^2 - 3x + a \, $ digeser ke kiri searah sumbu-x sejauh 2 satuan sehingga melalui titik (0,0), maka nilai $ a \, $ adalah ....
A). $ -2 $
B). $ -1 $
C). 0
D). 1
E). 2
5). Soal UTBK 2019 Soshum
jika kurva $ y = x^2 + 5x - 2p $ melalui titik $ (1,p) $ dan memotong sumbu X di $ (x_1, y_1) $ dan $ (x_2, y_2) $, maka nilai $ x_1^2 + y_1^2 + x_2^2 + y_2^2 = ... $
A). 31
B). 32
C). 33
D). 34
E). 35
Diketahui grafik fungsi $ f(x) = -x^2 + ax + b $ memotong sumbu X di titik $ (-p-3,0) $ dan titik $ (p,0) $ untuk suatu bilangan prima $ p $. Jika $ p + 3 $ juga merupakan suatu bilangan prima, maka nilai maksimum dari $ f(x) $ adalah ...
A). $ \frac{49}{2} \, $
B). $ \frac{49}{4} \, $
C). $ 10 \, $
D). $ -\frac{49}{4} \, $
E). $ -\frac{49}{2} $
Koordinat titik puncak grafik $ f(x) = ax^2 + bx + c $ adalah $ (4,2) $. Jika $ f(2) = 0 $, maka nilai $ 6a + b = ..... $
A). $ 5 \, $
B). $ 4 \, $
C). $ 3 \, $
D). $ 2 \, $
E). $ 1 $
Diketahui ordinat titik puncak fungsi kuadrat $ f(x) = ax^2 + bx + c \, $ adalah 2. Jika $ f(2) = f(4) = 0 \, $ maka $ a + b + c = .... $
A). $-10 \, $
B). $ -6 \, $
C). $ -4 \, $
D). $ 4 \, $
E). $ 6 $
Jika grafik fungsi $ y = x^2 - 9 \, $ memotong sumbu x di titik A dan B, serta memotong sumbu y di titik C, maka luas segitiga ABC adalah ....
A). 36
B). 33
C). 30
D). 27
E). 24
Tentu, beberapa contoh soal di atas masih terasa kurang jika benar-benar ingin menguasai berbagai variasi soal-soal Fungsi Kuadrat seleksi PTN. Untuk lebih memaksimalkan belajarnya, silahkan sahabat koma kunjungi link berikut :
Kumpulan soal Fungsi Kuadrat seleksi PTN .
Demikian pembahasan materi Ringkasan Fungsi Kuadrat Pertama Soshum - umptn dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan UMPTN (Ujian Masuk Perguruan Tinggi Negeri) bidang Matematika pada link Daftar Materi UMPTN Bidang Matematika. Jika ada saran atau kritikan atau lainnya yang sifatnya membangaun, silahkan untuk tulis komen pada kolom komentar dibagian bawah setiap artikel. Semoga artikel ini bermanfaat. Terimakasih.