Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas Solusi Singkat Soal OSK 2011 Bagian I Olim SMA sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMA. Dengan berlatih secara rutin dan giat dalam mempelajari
Soal dan Solusi Soal OSK-OSP-OSN Olim Matik SMA yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi Singkat Soal OSK 2011 Bagian I Olim SMA ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.
1). Misalkan kita menulis semua bilangan bulat 1, 2, 3, ..., 2011. Berapa kali kita menuliskan angka 1?
2). Sekelompok orang akan berjabat tangan. Setiap orang hanya dapat melakukan jabat tangan sekali. Tidak boleh melakukan jabat tangan dengan dirinya sendiri. Jika dalam sekelompok orang tersebut terdapat 190 jabat tangan, maka banyaknya orang dalam kelompok tersebut ada berapa?
3). Dalam suatu permainan, jika menang mendapat nilai 1, jika kalah mendapat nilai $-1$. $(a,b)$ menyatakan $a$ putaran permainan dan $b$ menyatakan total nilai seorang pemain, maka seluruh kemungkinan $(a,b)$ pada putaran ke-20 adalah ... ?
4). Di lemari hanya ada dua macam kaos kaki, yakni hitam dan putih. Ali, Budi, dan Candra berangkat di malam hari saat mati lampu, dan mereka mengambil kaus kaki secara acak dari lemari dalam kegelapan. Berapa kaus kaki minimal yang harus mereka ambil untuk memastikan bahwa akan ada 3 pasang kaus kaku yang bisa mereka pakai? (sepasang kaus kaki harus memiliki warna yang sama).
5). Misalkan batas suatu kebun dinyatakan dalam bentuk persamaan $|x+y|=400$ denga $x, y$ dinyatakan dalam satuan meter. Pemilik kebun setiap pagi biasa berjalan kaki berkeliling kebun dengan kecepatan $2\sqrt(2) $ km/jam searah jarum jam. Jika pemilik kebun pada pukul 6 berada di koordinat $(0,4)$, dimanakah posisi pemiliki kebuh pada pukul 06.06?
6). Ani mempunyai sangat banyak dadu ukuran $3 \times 3 \times 3 $ cm$^3$. Jika ia memasukkkan dadu-dadu tersebut ke dalam sebuah kardus dengan ukuran $50 \times 40 \times 35$ cm$^3$, maka berapa banyak dadu yang bisa masuk ke dalamnya?
7). Bilangan asli disusun seperti bagan di bawah ini.
$\begin{array}{cccccc} 1 & & & & & & \\ 2 & 3 & 4 & & & & \\ 5 & 6 & 7 & 8 & 9 & & \\ 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ \end{array} $
Bilangan ketiga pada baris ke-50 adalah ...?
8). Jumlah dari seluruh solusi persamaan $\sqrt[4]{x} = \frac{12}{7- \sqrt[4]{x} } $ adalah ...?
9). Enam dadu berbeda dilemparkan satu kali. Probabilitas jumlah mata dadu yang muncul 9 adalah ...?
10). Luas daerah di dalam lingkaran $x^2+y^2=21^2$ tetapi di luar lingkaran $x^2+(y-7)^2=12^2$ dan $x^2+(y+7)^2=14^2$ adalah ...?
1). Misalkan kita menulis semua bilangan bulat 1, 2, 3, ..., 2011. Berapa kali kita menuliskan angka 1?
2). Sekelompok orang akan berjabat tangan. Setiap orang hanya
dapat melakukan jabat tangan sekali. Tidak boleh melakukan
jabat tangan dengan dirinya sendiri. Jika dalam sekelompok
orang tersebut terdapat 190 jabat tangan, maka banyaknya
orang dalam kelompok tersebut ada berapa?
3). Dalam suatu permainan, jika menang mendapat nilai 1,
jika kalah mendapat nilai $-1$. $(a,b)$ menyatakan $a$
putaran permainan dan $b$ menyatakan total nilai seorang
pemain, maka seluruh kemungkinan $(a,b)$ pada putaran
ke-20 adalah ... ?
4). Di lemari hanya ada dua macam kaos kaki, yakni hitam
dan putih. Ali, Budi, dan Candra berangkat di malam hari saat
mati lampu, dan mereka mengambil kaus kaki secara acak dari
lemari dalam kegelapan. Berapa kaus kaki minimal yang harus
mereka ambil untuk memastikan bahwa akan ada 3 pasang kaus
kaku yang bisa mereka pakai? (sepasang kaus kaki harus
memiliki warna yang sama).
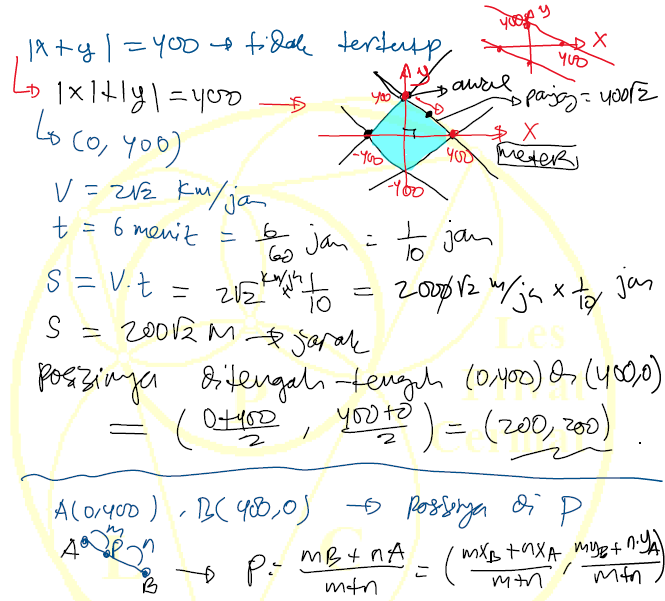
5). Misalkan batas suatu kebun dinyatakan dalam bentuk persamaan
$|x+y|=400$ denga $x, y$ dinyatakan dalam satuan meter.
Pemilik kebun setiap pagi biasa berjalan kaki berkeliling
kebun dengan kecepatan $2\sqrt(2) $ km/jam searah jarum jam.
Jika pemilik kebun pada pukul 6 berada di koordinat $(0,4)$,
dimanakah posisi pemiliki kebuh pada pukul 06.06?
Note: Soal ini seharusnya ada revisi yaitu $ |x| + |y| = 400 $ dan pada saat pukul 6 berada pada koordinat $(0, 400)$.
6). Ani mempunyai sangat banyak dadu ukuran
$3 \times 3 \times 3 $ cm$^3$. Jika ia memasukkkan
dadu-dadu tersebut ke dalam sebuah kardus dengan ukuran
$50 \times 40 \times 35$ cm$^3$, maka berapa banyak dadu
yang bisa masuk ke dalamnya?
7). Bilangan asli disusun seperti bagan di bawah ini.
$\begin{array}{cccccc} 1 & & & & & & \\ 2 & 3 & 4 & & & & \\ 5 & 6 & 7 & 8 & 9 & & \\ 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ \end{array} $
Bilangan ketiga pada baris ke-50 adalah ...?
8). Jumlah dari seluruh solusi persamaan
$\sqrt[4]{x} = \frac{12}{7- \sqrt[4]{x} } $ adalah ...?
9). Enam dadu berbeda dilemparkan satu kali. Probabilitas
jumlah mata dadu yang muncul 9 adalah ...?
10). Luas daerah di dalam lingkaran $x^2+y^2=21^2$ tetapi di luar
lingkaran $x^2+(y-7)^2=12^2$ dan $x^2+(y+7)^2=14^2$
adalah ...?
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2011 Bagian I Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.
Soal-soal Tanpa Solusi
1). Misalkan kita menulis semua bilangan bulat 1, 2, 3, ..., 2011. Berapa kali kita menuliskan angka 1?
2). Sekelompok orang akan berjabat tangan. Setiap orang hanya dapat melakukan jabat tangan sekali. Tidak boleh melakukan jabat tangan dengan dirinya sendiri. Jika dalam sekelompok orang tersebut terdapat 190 jabat tangan, maka banyaknya orang dalam kelompok tersebut ada berapa?
3). Dalam suatu permainan, jika menang mendapat nilai 1, jika kalah mendapat nilai $-1$. $(a,b)$ menyatakan $a$ putaran permainan dan $b$ menyatakan total nilai seorang pemain, maka seluruh kemungkinan $(a,b)$ pada putaran ke-20 adalah ... ?
4). Di lemari hanya ada dua macam kaos kaki, yakni hitam dan putih. Ali, Budi, dan Candra berangkat di malam hari saat mati lampu, dan mereka mengambil kaus kaki secara acak dari lemari dalam kegelapan. Berapa kaus kaki minimal yang harus mereka ambil untuk memastikan bahwa akan ada 3 pasang kaus kaku yang bisa mereka pakai? (sepasang kaus kaki harus memiliki warna yang sama).
5). Misalkan batas suatu kebun dinyatakan dalam bentuk persamaan $|x+y|=400$ denga $x, y$ dinyatakan dalam satuan meter. Pemilik kebun setiap pagi biasa berjalan kaki berkeliling kebun dengan kecepatan $2\sqrt(2) $ km/jam searah jarum jam. Jika pemilik kebun pada pukul 6 berada di koordinat $(0,4)$, dimanakah posisi pemiliki kebuh pada pukul 06.06?
6). Ani mempunyai sangat banyak dadu ukuran $3 \times 3 \times 3 $ cm$^3$. Jika ia memasukkkan dadu-dadu tersebut ke dalam sebuah kardus dengan ukuran $50 \times 40 \times 35$ cm$^3$, maka berapa banyak dadu yang bisa masuk ke dalamnya?
7). Bilangan asli disusun seperti bagan di bawah ini.
$\begin{array}{cccccc} 1 & & & & & & \\ 2 & 3 & 4 & & & & \\ 5 & 6 & 7 & 8 & 9 & & \\ 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ \end{array} $
Bilangan ketiga pada baris ke-50 adalah ...?
8). Jumlah dari seluruh solusi persamaan $\sqrt[4]{x} = \frac{12}{7- \sqrt[4]{x} } $ adalah ...?
9). Enam dadu berbeda dilemparkan satu kali. Probabilitas jumlah mata dadu yang muncul 9 adalah ...?
10). Luas daerah di dalam lingkaran $x^2+y^2=21^2$ tetapi di luar lingkaran $x^2+(y-7)^2=12^2$ dan $x^2+(y+7)^2=14^2$ adalah ...?
Soal-soal dengan Solusi Singkat
1). Misalkan kita menulis semua bilangan bulat 1, 2, 3, ..., 2011. Berapa kali kita menuliskan angka 1?
Note: Soal ini seharusnya ada revisi yaitu $ |x| + |y| = 400 $ dan pada saat pukul 6 berada pada koordinat $(0, 400)$.
$\begin{array}{cccccc} 1 & & & & & & \\ 2 & 3 & 4 & & & & \\ 5 & 6 & 7 & 8 & 9 & & \\ 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ \end{array} $
Bilangan ketiga pada baris ke-50 adalah ...?
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2011 Bagian I Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.