Garis Sumbu sebuah Segitiga
Garis sumbu sebuah segitiga adalah garis yang melalui titik tengah sisi segitiga dan
tegak lurus pada sisi tersebut. Perhatikan gambar garis sumbu berikut,
Dari gambar di atas, garis k sebagai garis sumbu sisi AC, garis l sebagai garis sumbu sisi AB, dan garis m sebagai
garis sumbu sisi BC.
Dalil-dalil yang berkaitan dengan garis sumbu yaitu :
Dalil 1 : Ketiga garis sumbu berpotongan pada satu titik yang disebut titik sumbu.
Dalil 2 : Titik sumbu segitiga berjarak sama ke setiap titik sudut segitiga,
Jarak OA = OB = OC.
Dalil 3 : Titik sumbu segitiga adalah titik pusat lingkaran luar segitiga seperti gambar berikut ini dengan titik P adalah titik sumbu pusat lingkaran,
Dalil-dalil yang berkaitan dengan garis sumbu yaitu :
Dalil 1 : Ketiga garis sumbu berpotongan pada satu titik yang disebut titik sumbu.
Dalil 2 : Titik sumbu segitiga berjarak sama ke setiap titik sudut segitiga,
Jarak OA = OB = OC.
Dalil 3 : Titik sumbu segitiga adalah titik pusat lingkaran luar segitiga seperti gambar berikut ini dengan titik P adalah titik sumbu pusat lingkaran,
Garis Tinggi sebuah Segitiga
Garis tinggi sebuah segitiga adalah garis yang melalui sebuah titik sudut segitiga dan tegak lurus pada sisi
yang berhadapan dengan titik sudut tersebut. perhatikan gambar garis tinggi berikut,
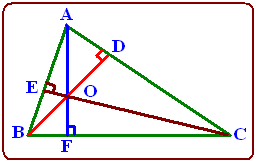
dari gambar, garis tingginya adalah garis AF, BD, dan CE. Ketiga garis tinggi berpotongan di titik O yang disebut dengan titik tinggi.
Menentukan panjang garis tinggi pada segitiga :
Untuk menentukan panjang garis tinggi, kita gunakan Dalil Proyeksi. Ada dua jenis yaitu :
*). Dali proyeksi segitiga lancip,
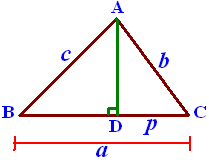
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.
Misalkan panjang $ CD = p \, $ ,
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 - 2ap $
Misalkan panjang $ BD = k \, $ ,
panjang $ k $ bisa ditentukan dengan rumus: $ \, b^2 = a^2 + c^2 - 2ap $
*). Dali proyeksi segitiga tumpul,
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.
Misalkan panjang $ BD = p \, $ ,
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 + 2ap $
Catatan :
*). Dalil proyeksi ini bisa kita gunakan untuk membuktikan dalil Stewart.
*). Untuk contoh dan pembuktian garis tinggi, lilahkan baca lebih lengkap di "Garis Tinggi dan Pembuktiannya".
Menentukan panjang garis tinggi pada segitiga :
Untuk menentukan panjang garis tinggi, kita gunakan Dalil Proyeksi. Ada dua jenis yaitu :
*). Dali proyeksi segitiga lancip,
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 - 2ap $
Misalkan panjang $ BD = k \, $ ,
panjang $ k $ bisa ditentukan dengan rumus: $ \, b^2 = a^2 + c^2 - 2ap $
*). Dali proyeksi segitiga tumpul,
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 + 2ap $
Catatan :
*). Dalil proyeksi ini bisa kita gunakan untuk membuktikan dalil Stewart.
*). Untuk contoh dan pembuktian garis tinggi, lilahkan baca lebih lengkap di "Garis Tinggi dan Pembuktiannya".
Garis Berat sebuah Segitiga
Garis berat sebuah segitiga adalah garis yang melalui sebuah titik sudut dan membagi sisi didepan sudut menjadi dua
bagian sama panjang. Perhatikan gambar garis berat berikut,
dari gambar di atas, garis beratnya adalah AD, BE, dan CF. Perpotongan ketiga garis berat disebut titik berat. Ketiga garis berat berpotongan di titik
berat dengan perbandingan panjang 2 : 1 ,
yaitu AO : OD = BO : OE = CO : OF = 2 : 1.
Menentukan panjang garis beratnya.
perhatikan gambar gari berat AD berikut,
Misalkan panjang $ AD = d \, $,
menentukan panjang garis berat dengan rumus :
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2} - \frac{1}{4}a^2 $.
Untuk contoh dan pembuktian panjang garis berat, silahkan baca secara lengkap pada artikel "Garis Berat dan Pembuktiannya".
yaitu AO : OD = BO : OE = CO : OF = 2 : 1.
Menentukan panjang garis beratnya.
perhatikan gambar gari berat AD berikut,
menentukan panjang garis berat dengan rumus :
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2} - \frac{1}{4}a^2 $.
Untuk contoh dan pembuktian panjang garis berat, silahkan baca secara lengkap pada artikel "Garis Berat dan Pembuktiannya".
Garis Bagi sebuah Segitiga
Garis bagi sebuah segitiga adalah garis yang ditarik dari titik sudut segitiga memotong sisi didepan titik sudut
tersebut dengan membagi dua sama besar suudut tersebut, seperti gambar berikut.
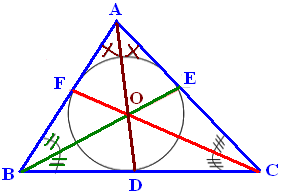
Dari gambar gari sbagi di atas, garis baginya adalah garis AD, BE, dan CF. Ketiga gari bagi berpotongan di titik O yang disebut dengan titik bagi. Garis
bagi membagi sisi di depannya menjadi dua bagian dengan rasio panjangnya sama dengan rasio sisi-sisi bergekatan (misalkan BD : DC = BA : AC).
Titik bagi sebuah segitiga merupakan titik pusat lingkaran dalam segitiga seperti gambar berikut.
Menentukan panjang garis bagi.
perhatikan gambar garis bagi berikut,
Misalkan panjang garis bagi $ AD = d , \, $
menentukan panjang $ d \, $ dengan rumus :
$ d^2 = bc - mn $
dengan $ m : n = c : b $
sehingga $ m = \frac{c}{ b+ c} \times a \, $ dan $ n = \frac{b}{ b+ c} \times a $
Untuk contoh dan pembuktian panjang garis bagi, silahkan baca secara lengkap pada artikel "Garis Bagi dan Pembuktiannya".
Menentukan panjang garis bagi.
perhatikan gambar garis bagi berikut,
menentukan panjang $ d \, $ dengan rumus :
$ d^2 = bc - mn $
dengan $ m : n = c : b $
sehingga $ m = \frac{c}{ b+ c} \times a \, $ dan $ n = \frac{b}{ b+ c} \times a $
Untuk contoh dan pembuktian panjang garis bagi, silahkan baca secara lengkap pada artikel "Garis Bagi dan Pembuktiannya".
