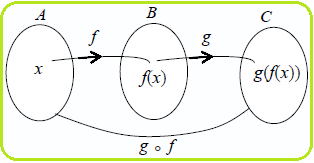
Definisi Daerah Asal (Domain) Komposisi Fungsi
*). Misalkan terdefinisi fungsi komposisi $ (g \circ f)(x) \, $ , daerah asalnya ($D_{g \circ f}$) adalah
$ D_{g \circ f} = \{ x | x \in D_f , \, f(x) \in D_g \} $
*). Misalkan terdefinisi fungsi komposisi $ (f \circ g)(x) \, $ , daerah asalnya ($D_{f \circ g}$) adalah $ D_{f \circ g} = \{ x | x \in D_g , \, g(x) \in D_f \} $
Keterangan :
$ D_f = \, $ daerah asal fungsi $ f $
$ D_g = \, $ daerah asal fungsi $ g $
*). Misalkan terdefinisi fungsi komposisi $ (f \circ g)(x) \, $ , daerah asalnya ($D_{f \circ g}$) adalah $ D_{f \circ g} = \{ x | x \in D_g , \, g(x) \in D_f \} $
Keterangan :
$ D_f = \, $ daerah asal fungsi $ f $
$ D_g = \, $ daerah asal fungsi $ g $
Dari definisi Daerah Asal Komposisi Fungsi di atas, kita akan dapat menentukan daerah asalnya. Hanya saja untuk aplikasinya menurut kami tidaklah mudah. Maka dari itu, kita akan memodifikasi definisi di atas dengan hasil yang sama tentunya. Berikut cara "Menentukan Daerah Asal Komposisi Fungsi" :
Menentukan Daerah Asal Komposisi Fungsi
$ \clubsuit \, $ Menentukan daerah asal $ g \circ f $ :
Misalkan terdefinisi fungsi komposisi $ p = (g \circ f)(x) \, $ ,
daerah asal $ g \circ f $ : $ D_{g \circ f} = \{ x | x \in ( D_f \cap D_p ) \} $
$ \spadesuit \, $ Menentukan daerah asal $ f \circ g $ :
Misalkan terdefinisi fungsi komposisi $ q = (f \circ g)(x) \, $ ,
daerah asal $ f \circ g $ : $ D_{f \circ g} = \{ x | x \in ( D_g \cap D_q) \} $
Misalkan terdefinisi fungsi komposisi $ p = (g \circ f)(x) \, $ ,
daerah asal $ g \circ f $ : $ D_{g \circ f} = \{ x | x \in ( D_f \cap D_p ) \} $
$ \spadesuit \, $ Menentukan daerah asal $ f \circ g $ :
Misalkan terdefinisi fungsi komposisi $ q = (f \circ g)(x) \, $ ,
daerah asal $ f \circ g $ : $ D_{f \circ g} = \{ x | x \in ( D_g \cap D_q) \} $
Sebelum kita membahas contoh-contoh soalnya, kita ingat kembali beberapa bentuk fungsi dan daerah asalnya berikut ini yaitu :
a). Fungsi $ f(x) = a_nx^n + a_{n-1}x^{n-1} + ...+ a_1x + a_0 $ (fungsi polinomial)
Daerah asalnya : $ D_f = \{ x | x \in R \} $
b). Fungsi $ f(x) = \sqrt{ g(x)} $ (fungsi bentuk akar/irrasional)
Daerah asalnya : $ D_f = \{ x | g(x) \geq 0 \} $
c). Fungsi $ f(x) = \frac{h(x)}{g(x)} $ (fungsi bentuk pecahan/rasional)
Daerah asalnya : $ D_f = \{ x | g(x) \neq 0 \} $
d). Fungsi $ f(x) = {}^a \log g(x) $ (fungsi bentuk logaritma)
Daerah asalnya : $ D_f = \{ x | g(x) > 0 \} $
e). Fungsi $ f(x) = \sin g(x) $ (fungsi bentuk trigonometri)
Daerah asalnya : $ D_f = \{ x | x \in R \} $
Catatan : yang dimaksud dengan daerah asal (domain fungsi) adalah semua nilai $ x $ yang bisa kita substitusikan ke fungsinya dan fungsinya bernilai real (untuk tingkat SMA, batasan bilangannya biasanya sampai bilangan real saja). Atau dengan kata lain, fungsinya bisa kita hitung dengan nilai $ x $ yang kita substitusikan.
Contoh Soal Daerah Asal Komposisi Fungsi :
1). Diketahui fungsi $ f(x) = 2x - 3 $ dan $ g(x) = x^2 + 1 $. Tentukan :
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Penyelesaian :
*). Domain fungsi $ f(x) = 2x - 3 $ (polinomial) : $ D_f = \{ x \in R \} $
*). Domain fungsi $ g(x) = x^2 + 1 $ (polinomial) : $ D_g = \{ x \in R \} $
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
Misalkan $ p = (g \circ f) (x) $
$ p = (g \circ f) (x) = g(f(x)) = g (2x-3) = (2x -3)^2 + 1 = 4x^2 -12x + 10 $.
Domain dari $ p = 4x^2 -12x + 10 $ adalah $ D_p = \{ x \in R \} $ .
*). Domain $ (g \circ f) (x) $ :
$ D_{g \circ f} = D_f \cap D_p = \{ x \in R \} \cap \{ x \in R \} = \{ x \in R \} $
Sehingga daerah asal dari $ (g \circ f) (x) $ adalah $ \{ x \in R \} $ .
atau dapat kita tulis $ -\infty < x < \infty $.
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Misalkan $ q = (f \circ g) (x) $
$ q = (f \circ g) (x) = f(g(x)) = f( x^2 +1) = 2(x^2 + 1) - 3 = 2x^2 -1 $.
Domain dari $ q = x^2 -1 $ adalah $ D_q = \{ x \in R \} $ .
*). Domain $ (f \circ g) (x) $ :
$ D_{f \circ g} = D_g \cap D_q = \{ x \in R \} \cap \{ x \in R \} = \{ x \in R \} $
Sehingga daerah asal dari $ (f \circ g) (x) $ adalah $ \{ x \in R \} $ .
atau dapat kita tulis $ -\infty < x < \infty $.
2). Diketahui fungsi $ f(x) = x^2 - 1 $ dan $ g(x) = \sqrt{ x - 3} $. Tentukan :
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Penyelesaian :
*). Domain fungsi $ f(x) = x^2 - 1 $ (polinomial) : $ D_f = \{ x \in R \} $
*). Domain fungsi $ g(x) = \sqrt{ x - 3} $
$ x - 3 \geq 0 \rightarrow x \geq 3 $ : $ D_g = \{ x \geq 3 \} $
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
Misalkan $ p = (g \circ f) (x) $
$ p = (g \circ f) (x) = g (x^2 - 1) = \sqrt{ (x^2 -1) - 3} = \sqrt{ x^2 - 4} $.
Domain dari $ p = \sqrt{ x^2 - 4} $
$ x^2 - 4 \geq 0 $ : $ D_p = \{ x \leq -2 \vee x \geq 2 \} $ .
*). Domain $ (g \circ f) (x) $ :
$ D_{g \circ f} = D_f \cap D_p = \{ x \in R \} \cap \{ x \leq -2 \vee x \geq 2 \} = \{ x \leq -2 \vee x \geq 2 \} $
Sehingga daerah asal dari $ (g \circ f) (x) $ adalah $ \{ x \leq -2 \vee x \geq 2 \} $ .
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Misalkan $ q = (f \circ g) (x) $
$ q = (f \circ g) (x) = f( \sqrt{ x - 3}) = (\sqrt{ x - 3})^2 - 1 = x - 4 $.
Domain dari $ q = x - 4 $ adalah $ D_q = \{ x \in R \} $ .
*). Domain $ (f \circ g) (x) $ :
$ D_{f \circ g} = D_g \cap D_q = \{ x \geq 3 \} \cap \{ x \in R \} = \{ x \geq 3 \} $
Sehingga daerah asal dari $ (f \circ g) (x) $ adalah $ \{ x \geq 3 \} $ .
Catatan :
Untuk menyelesaikan bentu pertidaksamaan, silahkan teman-teman baca artikelnya pada :
"Pertidaksamaan secara Umum", "Pertidaksamaan Linear", "Pertidaksamaan Kuadrat", "Pertidaksamaan Pecahan", dan "Pertidaksamaan Bentuk Akar".
3). Diketahui fungsi $ f(x) = \sqrt{x + 1} $ dan $ g(x) = \sqrt{ 4 - x^2} $. Tentukan :
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Penyelesaian :
*). Domain fungsi $ f(x) = \sqrt{x + 1} $
$ x + 1 \geq 0 \rightarrow x \geq -1 $ : $ D_f = \{ x \geq -1 \} $
*). Domain fungsi $ g(x) = \sqrt{ 4 - x^2} $
$ 4 - x^2 \geq 0 $ : $ D_g = \{ -2 \leq x \leq 2 \} $
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
Misalkan $ p = (g \circ f) (x) $
$ p = (g \circ f) (x) = g (\sqrt{x + 1}) = \sqrt{4 - (\sqrt{x + 1})^2} = \sqrt{ 3 - x} $.
Domain dari $ p = \sqrt{ 3 - x } $
$ 3 - x \geq 0 \rightarrow x \leq 3 $ : $ D_p = \{ x \leq 3 \} $ .
*). Domain $ (g \circ f) (x) $ :
$ D_{g \circ f} = D_f \cap D_p = \{ x \geq -1 \} \cap \{ x \leq 3 \} = \{ -1 \leq x \leq 3 \} $
Sehingga daerah asal dari $ (g \circ f) (x) $ adalah $ \{ -1 \leq x \leq 3 \} $ .
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Misalkan $ q = (f \circ g) (x) $
$ q = (f \circ g) (x) = f( \sqrt{ 4 - x^2}) = \sqrt{\sqrt{ 4 - x^2} + 1} $.
Domain dari $ q = \sqrt{\sqrt{ 4 - x^2} + 1} $
$ \sqrt{ 4 - x^2} + 1 \geq 0 \rightarrow \sqrt{ 4 - x^2} \geq -1 \rightarrow \sqrt{ 4 - x^2} \geq 0 \rightarrow 4 - x^2 \geq 0 $
adalah $ D_q = \{ -2 \leq x \leq 2 \} $ .
*). Domain $ (f \circ g) (x) $ :
$ D_{f \circ g} = D_g \cap D_q = \{ -2 \leq x \leq 2 \} \cap \{ -2 \leq x \leq 2 \} = \{ -2 \leq x \leq 2 \} $
Sehingga daerah asal dari $ (f \circ g) (x) $ adalah $ \{ -2 \leq x \leq 2 \} $ .
4). Diketahui fungsi $ f(x) = 3x + 1 $ dan $ g(x) = \frac{2x - 3 }{x + 1} $. Tentukan :
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Penyelesaian :
*). Domain fungsi $ f(x) = 3x + 1 $ : $ D_f = \{ x \in R \} $
*). Domain fungsi $ g(x) = \frac{2x - 3 }{x + 1} $
$ x + 1 \neq 0 \rightarrow x \neq -1 $ : $ D_g = \{ x \neq -1 \} $
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
Misalkan $ p = (g \circ f) (x) $
$ p = (g \circ f) (x) = g (3x + 1) = \frac{2(3x + 1) - 3 }{3x + 1 + 1} = \frac{6x - 1}{3x + 2} $.
Domain dari $ p = \frac{6x - 1}{3x + 2} $
$ 3x + 2 \neq 0 \rightarrow x \neq - \frac{2}{3} $ : $ D_p = \{ x \neq - \frac{2}{3} \} $ .
*). Domain $ (g \circ f) (x) $ :
$ D_{g \circ f} = D_f \cap D_p = \{ x \in R \} \cap \{ x \neq - \frac{2}{3} \} = \{ x \neq - \frac{2}{3} \} $
Sehingga daerah asal dari $ (g \circ f) (x) $ adalah $ \{ x \neq - \frac{2}{3} \} $ .
atau dapat ditulis $ \{ x < - \frac{2}{3} \, \text{ atau } \, x > - \frac{2}{3} \} $ .
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Misalkan $ q = (f \circ g) (x) $
$ q = (f \circ g) (x) = f( \frac{2x - 3 }{x + 1}) = 3\left( \frac{2x - 3 }{x + 1}\right) + 1 = \frac{7x - 8}{ x + 1} $.
Domain dari $ q = \frac{7x - 8}{ x + 1} $
$ x + 1 \neq 0 \rightarrow x \neq -1 $ adalah $ D_q = \{ x \neq -1 \} $ .
*). Domain $ (f \circ g) (x) $ :
$ D_{f \circ g} = D_g \cap D_q = \{ x \neq -1 \} \cap \{ x \neq -1 \} = \{ x \neq -1 \} $
Sehingga daerah asal dari $ (f \circ g) (x) $ adalah $ \{ x \neq -1 \} $ .
atau dapat kita tulis $ \{ x < - 1 \, \text{ atau } \, x > - 1 \} $
5). Diketahui fungsi $ f(x) = \frac{3}{x-1} $ dan $ g(x) = \frac{2x }{3x - 2} $. Tentukan :
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Penyelesaian :
*). Domain fungsi $ f(x) = \frac{3}{x-1} $
$ x - 1 \neq 0 \rightarrow x \neq 1 $ : $ D_f = \{ x \neq 1 \} $
*). Domain fungsi $ g(x) = \frac{2x }{3x - 2} $
$ 3x - 2 \neq 0 \rightarrow x \neq \frac{3}{2} $ : $ D_g = \{ x \neq \frac{2}{3} \} $
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
Misalkan $ p = (g \circ f) (x) $
$ p = (g \circ f) (x) = g (\frac{3}{x-1}) = \frac{2.\frac{3}{x-1} }{3.\frac{3}{x-1}- 2} = \frac{6}{11 - 2x} $.
Domain dari $ p = \frac{6}{11 - 2x} $
$ 11 - 2x \neq 0 \rightarrow x \neq \frac{11}{2} $ : $ D_p = \{ x \neq \frac{11}{2} \} $ .
*). Domain $ (g \circ f) (x) $ :
$ D_{g \circ f} = D_f \cap D_p = \{ x \neq 1 \} \cap \{ x \neq \frac{11}{2} \} = \{ x \neq 1 \, \text{ dan } \, x \neq \frac{11}{2} \} $
Sehingga daerah asal dari $ (g \circ f) (x) $ adalah $ \{ x \neq 1 \, \text{ dan } \, x \neq \frac{11}{2} \} $ .
atau dapat ditulis $ \{ x < 1 \, \text{ atau } \, 1 < x < \frac{11}{2} \, \text{ atau } \, x > \frac{11}{2} \} $ .
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Misalkan $ q = (f \circ g) (x) $
$ q = (f \circ g) (x) = f( \frac{2x }{3x - 2} ) = \frac{3}{\frac{2x }{3x - 2} -1} = \frac{9x - 6}{ -x + 2} $.
Domain dari $ q = \frac{9x - 6}{ -x + 2} $
$ -x + 2 \neq 0 \rightarrow x \neq 2 $ adalah $ D_q = \{ x \neq 2 \} $ .
*). Domain $ (f \circ g) (x) $ :
$ D_{f \circ g} = D_g \cap D_q = \{ x \neq \frac{2}{3} \} \cap \{ x \neq 2 \} = \{ x \neq \frac{2}{3} \, \text{ dan } \, x \neq 2 \} $
Sehingga daerah asal dari $ (f \circ g) (x) $ adalah $ \{ x \neq \frac{2}{3} \, \text{ dan } \, x \neq 2 \} $ .
atau dapat kita tulis $ \{ x < \frac{2}{3} \, \text{ atau } \, \frac{2}{3} < x < 2 \, \text{ atau } \, x > 2 \} $ .
6). Diketahui fungsi $ f(x) = \frac{4}{x^2-1} $ dan $ g(x) = \sqrt{ x + 4} $. Tentukan :
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Penyelesaian :
*). Domain fungsi $ f(x) = \frac{4}{x^2-1} $
$ x^2-1 \neq 0 \rightarrow x \neq -1 , x \neq 1 $ : $ D_f = \{ x \neq -1 , x \neq 1 \} $
*). Domain fungsi $ g(x) = \sqrt{ x + 4} $
$ x + 4 \geq 0 \rightarrow x \geq -4 $ : $ D_g = \{ x \geq -4 \} $
a). daerah asal komposisi fungsi $ (g \circ f) (x) $
Misalkan $ p = (g \circ f) (x) $
$ p = (g \circ f) (x) = g (\frac{4}{x^2-1} ) = \sqrt{\frac{4}{x^2-1} + 4} = \sqrt{ \frac{4x^2}{x^2 - 1}} $.
Domain dari $ p = \sqrt{ \frac{4x^2}{x^2 - 1}} $
$ \frac{4x^2}{x^2 - 1} \geq 0 $ : $ D_p = \{ x < -1 \vee x > 1 \} $ .
*). Domain $ (g \circ f) (x) $ :
$ D_{g \circ f} = D_f \cap D_p = \{ x \neq -1 , x \neq 1 \} \cap \{ x < -1 \vee x > 1 \} = \{ x < -1 \vee x > 1 \} $
Sehingga daerah asal dari $ (g \circ f) (x) $ adalah $ \{ x < -1 \vee x > 1 \} $ .
b). daerah asal komposisi fungsi $ (f \circ g) (x) $
Misalkan $ q = (f \circ g) (x) $
$ q = (f \circ g) (x) = f(\sqrt{ x + 4}) = \frac{4}{(\sqrt{x + 4})^2-1} = \frac{4}{x + 3} $.
Domain dari $ q = \frac{4}{x + 3} $
$ x + 3 \neq 0 \rightarrow x \neq -3 $ adalah $ D_q = \{ x \neq -3 \} $ .
*). Domain $ (f \circ g) (x) $ :
$ D_{f \circ g} = D_g \cap D_q = \{ x \geq -4 \} \cap \{ x \neq -3 \} = \{ x \geq -4 \, \text{ dan } \, x \neq -3 \} $
Sehingga daerah asal dari $ (f \circ g) (x) $ adalah $ \{ x \geq -4 \, \text{ dan } \, x \neq -3 \} $ .
atau dapat kita tulis $ \{ -4 \leq x < -3 \, \text{ atau } \, x > -3 \} $ .
Daerah Hasil (Range) Komposisi Fungsi
Untuk menentukan daerah hasil suatu bentuk fungsi atau bentuk komposisi fungsi yaitu dengan mensubstitusikan daerah
asal yang terbentuk. Namun kita juga harus tetap memperhatikan karakteristik masing-masing fungsinya, semisal fungsi kuadrat memiliki nilai maksimum atau
minimum tertentu, sementara fungsi bentuk akar memiliki nilai fungsi yang selalu positif. dan karakteristik fungsi lainnya.
Untuk memudahkan dalam penghitungan, kita akan langsung coba mencari daerah hasil komposisi fungsi pada contoh-contoh soal di atas.
7). Diketahui fungsi $ f(x) = 2x - 3 $ dan $ g(x) = x^2 + 1 $. Tentukan :
a). daerah hasil komposisi fungsi $ (g \circ f) (x) $
b). daerah hasil komposisi fungsi $ (f \circ g) (x) $
(contoh nomor 6)
Penyelesaian :
a). daerah hasil komposisi fungsi $ (g \circ f) (x) $
*). Telah kita peroleh :
$ (g \circ f) (x) = 4x^2 -12x + 10 $,
Domain : $ -\infty < x < \infty $,
*). Menentukan daerah hasilnya :
$ y = (g \circ f) (x) = 4x^2 -12x + 10 = 4(x - \frac{3}{2} )^2 + 1 $
Dari bentuk $ y = 4(x - \frac{3}{2} )^2 + 1 $ nilai minimumnya saat $ x = \frac{3}{2} $ yaitu $ y = 1 $
Sehingga daerah hasilnya adalah $ \{ y | y \geq 1 \} $.
b). daerah hasil komposisi fungsi $ (f \circ g) (x) $
*). Telah kita peroleh :
$ (f \circ g) (x) = 2x^2 -1 $,
Domain : $ -\infty < x < \infty $,
*). Menentukan daerah hasilnya :
$ y = (f \circ g) (x) = 2x^2 -1 $
Dari bentuk $ y = 2x^2 -1 $ nilai minimumnya saat $ x = 0 $ yaitu $ y = -1 $
Sehingga daerah hasilnya adalah $ \{ y | y \geq - 1 \} $.
8). Diketahui fungsi $ f(x) = x^2 - 1 $ dan $ g(x) = \sqrt{ x - 3} $. Tentukan :
a). daerah hasil komposisi fungsi $ (g \circ f) (x) $
b). daerah hasil komposisi fungsi $ (f \circ g) (x) $
(contoh nomor 6)
Penyelesaian :
a). daerah hasil komposisi fungsi $ (g \circ f) (x) $
*). Telah kita peroleh :
$ (g \circ f) (x) = \sqrt{x^2 - 4} $,
Domain : $ x \leq -2 \vee x \geq 2 $,
*). Menentukan daerah hasilnya :
$ y = (g \circ f) (x) = \sqrt{x^2 - 4} $
Dari bentuk $ y = \sqrt{x^2 - 4} $ nilai minimumnya saat $ x = -2 $ atau $ x = 2 $ yaitu $ y = 0 $
Sehingga daerah hasilnya adalah $ \{ y | y \geq 0 \} $.
b). daerah hasil komposisi fungsi $ (f \circ g) (x) $
*). Telah kita peroleh :
$ (f \circ g) (x) = x - 4 $,
Domain : $ x \geq 3 $,
*). Menentukan daerah hasilnya :
$ y = (f \circ g) (x) = x - 4 $
Dari bentuk $ y = x - 4 $ nilai minimumnya saat $ x = 3 $ yaitu $ y = -1 $
Sehingga daerah hasilnya adalah $ \{ y | y \geq - 1 \} $.
cara lain untuk bagian (a) dan (b) nomor (8) ini yaitu :
a). $ y = \sqrt{x^2 - 4}$
$ x \leq -2 \rightarrow x^2 \geq 4 \rightarrow x^2 - 4 \geq 0 \rightarrow \sqrt{x^2 - 4} \geq 0 \rightarrow y \geq 0 $
$ x \geq 2 \rightarrow x^2 \geq 4 \rightarrow x^2 - 4 \geq 0 \rightarrow \sqrt{x^2 - 4} \geq 0 \rightarrow y \geq 0 $
b). $ y = x - 4 $
$ x \geq 3 \rightarrow x - 4 \geq 3 - 4 \rightarrow x - 4 \geq -1 \rightarrow y \geq -1 $.
Untuk contoh yang lainnya silahkan teman-teman coba sendiri ya. Semoga bisa dan benar.
$ \spadesuit \, $ Pembuktian Menentukan Daerah Asal Komposisi Fungsi
Perhatikan definisi daerah asal komposisi fungsi pada artikel paling atas dan definisi "fungsi invers" berikut ini.
Definisi fungsi invers : $ f(A) = B \leftrightarrow A = f^{-1}(B) $.
dari definisi invers fungsi $ f $ ini , A sebagai domain dan B sebagai range dimana $ f^{-1}(B) = A $ artinya $ f^{-1}{B} $ menghasikan domain dari fungsi $ f $ yaitu A.
*). Pembuktian pertama : Menentukan daerah asal $ g \circ f $ :
Misalkan terdefinisi fungsi komposisi $ p = (g \circ f)(x) \, $ ,
daerah asal $ g \circ f $ : $ D_{g \circ f} = \{ x | x \in ( D_f \cap D_p ) \} $
-). Misalkan terdapat $ p $ yang merupakan daerah hasil dari $ (g \circ f)(x) $ atau bisa kita tulis $ p = (g \circ f)(x) $. Karena $ p $ daerah hasil $ (g \circ f)(x) $, maka $ p $ juga merupakan daerah hasil dari fungsi $ g $ , sehingga daerah asal dari $ g $ adalah $ g^{-1}(p) $ sesuai definisi invers di atas.
-). Dari definisi : $ D_{g \circ f} = \{ x | x \in D_f , \, f(x) \in D_g \} $
bentuk $ f(x) \in D_g $ artinya terdapat $ x $ sehingga nilai fungsi $ f(x) $ ada yang sama dengan anggota dari domain fungsi $ g $, misalkan domain $ g $ yang memenuhi tersebut adalah $ g^{-1}(p) $. Dapat kita tulis $ f(x) = g^{-1}(p) $. Dari definisi invers fungsi :
$ f(x) = g^{-1}(p) \rightarrow p = g(f(x)) \rightarrow p = ( g \circ f)(x) \, $ .....(i)
Dari bentuk (i) ini, artinya $ x $ adalah domain dari fungsi $ p = ( g \circ f)(x) $ atau kita tulis $ x \in D_p $.
-). Pada definisi : $ x \in D_f $. Di lain pihak juga $ x \in D_p $ , sehingga dapat kita simpulkan $ x \in ( D_f \cap D_p) $.
Jadi, terbukti bahwa $ D_{g \circ f} = \{ x | x \in ( D_f \cap D_p ) \} $
*). Pembuktian kedua : Menentukan daerah asal $ f \circ g $ :
Misalkan terdefinisi fungsi komposisi $ q = (f \circ g)(x) \, $ ,
daerah asal $ f \circ g $ : $ D_{f \circ g} = \{ x | x \in ( D_g \cap D_q) \} $
-). Misalkan terdapat $ q $ yang merupakan daerah hasil dari $ (f \circ g)(x) $ atau bisa kita tulis $ q = (f \circ g)(x) $. Karena $ q $ daerah hasil $ (f \circ g)(x) $, maka $ q $ juga merupakan daerah hasil dari fungsi $ f $ , sehingga daerah asal dari $ f $ adalah $ f^{-1}(q) $ sesuai definisi invers di atas.
-). Dari definisi : $ D_{f \circ g} = \{ x | x \in D_g , \, g(x) \in D_f \} $
bentuk $ g(x) \in D_f $ artinya terdapat $ x $ sehingga nilai fungsi $ g(x) $ ada yang sama dengan anggota dari domain fungsi $ f $, misalkan domain $ f $ yang memenuhi tersebut adalah $ f^{-1}(q) $. Dapat kita tulis $ g(x) = f^{-1}(q) $. Dari definisi invers fungsi :
$ g(x) = f^{-1}(q) \rightarrow q = f(g(x)) \rightarrow q = ( f \circ g)(x) \, $ .....(ii)
Dari bentuk (ii) ini, artinya $ x $ adalah domain dari fungsi $ q = ( f \circ g)(x) $ atau kita tulis $ x \in D_q $.
-). Pada definisi : $ x \in D_g $. Di lain pihak juga $ x \in D_q $ , sehingga dapat kita simpulkan $ x \in ( D_g \cap D_q) $.
Jadi, terbukti bahwa $ D_{f \circ g} = \{ x | x \in ( D_g \cap D_q) \} $
Demikian pembahasan materi Daerah Asal dan Daerah Hasil Komposisi Fungsi dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan "fungsi".