Untuk memudahkan dalam mempelajari materi Menentukan Panjang Busur dengan Integral, teman-teman harus menguasai terlebih dahulu materi jarak dua titik, jumlah Riemann, turunan fungsi aljabar, dan integral tentu fungsi baik aljabar maupun trigonometri. Sebenarnya secara teori materi panjang busur ini sangatlah mudah, hanya saja penggunaan dalam soalnya lebih sulit terutama untuk menghitung hasil integralnya.
Menentukan Panjang Busur dengan Integral maksudnya kita akan menghitung panjang suatu busur pada batas interval tertentu dari kurva yang nampak. Perhatikan gambar ilustrasi berikut ini, kita akan menghitung panjang busur dari kurva fungsi $ y = f(x) \, $ dari interval $ a \leq x \leq b \, $ atau $ c \leq y \leq d \, $ :
jarak $ = \sqrt{(x_k - x_{k-1})^2 + (y_k - y_{k-1})^2 } = \sqrt{(\Delta x_k )^2 + ( \Delta y_k )^2 } $.
Artinya panjang total busur dengan pendekatan garis yaitu :
Panjang busur (pendekatan) $ \, = \displaystyle \sum_{k=1}^{n} \sqrt{(\Delta x_k )^2 + ( \Delta y_k )^2 } $ .
Jika kita ambil nilai $ \Delta x_k \, $ dan $ \Delta y_k \, $ sekecil mungkin, artinya banyaknya garis-garis lurus kecil-kecil sependek mungkin yang kita peroleh untuk $ n \, $ mendekati tak hingga, sehingga panjang busur dapat dirumuskan :
Panjang busur $ \, = \displaystyle \lim_{n \to \infty} \sum_{k=1}^{n} \sqrt{(\Delta x_k )^2 + ( \Delta y_k )^2 } \, $ atau dengan jumlah Riemann
Panjang busur $ \, = \displaystyle \lim_{n \to \infty} \sum_{k=1}^{n} \sqrt{ 1 + \left( \frac{\Delta y_k}{\Delta x_k} \right)^2 } \, \Delta x_k = \int \limits_a^b \sqrt{ 1 + \left( \frac{dy}{dx} \right)^2 } \, dx \, $ atau
Panjang busur $ \, = \displaystyle \lim_{n \to \infty} \sum_{k=1}^{n} \sqrt{ \left( \frac{\Delta x_k}{\Delta y_k} \right)^2 + 1 } \, \, \Delta y_k = \int \limits_c^d \sqrt{ \left( \frac{dx}{dy} \right)^2 + 1 } \, \, dy $.
Bagaimana dengan teori di atas, pasti terlihat sulit yah? iya, karena kita coba untuk menemukan bagaimana asal dari rumus atau cara penghitungan panjang busur suatu kurva menggunakan integral. Berikut akan kita tulis rangkuman secara lebih sederhana rumus panjang busur suatu kurva.
Rumus Menentukan Panjang Busur dengan Integral
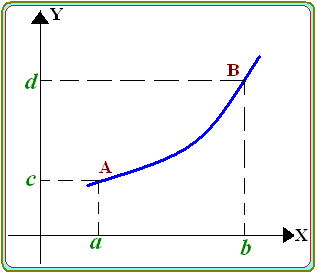
Perhatikan gambar kurva berikut ini,
Panjang busur kurva $ y = f(x) \, $ dari titik $ A(a,c) \, $ ke titik $ B(b,d) \, $ dapat dihitung dengan rumus :
*). Berdasarkan batasan sumbu X :
panjang busur AB $ \, = \int \limits_a^b \sqrt{ 1 + \left( \frac{dy}{dx} \right)^2 } \, dx $
*). Berdasarkan batasan sumbu Y :
panjang busur AB $ \, = \int \limits_c^d \sqrt{ \left( \frac{dx}{dy} \right)^2 + 1 } \, \, dy $ .
*). Berdasarkan batasan sumbu X :
panjang busur AB $ \, = \int \limits_a^b \sqrt{ 1 + \left( \frac{dy}{dx} \right)^2 } \, dx $
*). Berdasarkan batasan sumbu Y :
panjang busur AB $ \, = \int \limits_c^d \sqrt{ \left( \frac{dx}{dy} \right)^2 + 1 } \, \, dy $ .
1). Tentukan panjang busur kurva $ 9y^2 = 4x^3 \, $ dari titik $ A(0,0) \, $ ke titik $ B(3, 2\sqrt{3}) $ ?
Penyelesaian :
*). Kita ubah dulu fungsinya :
$ 9y^2 = 4x^3 \rightarrow y = \sqrt{\frac{4x^3}{9}} = \frac{2}{3} x^\frac{3}{2} $
*). Menentukan turunannya :
$ \frac{dy}{dx} = \frac{2}{3} . \frac{3}{2} x^{\frac{3}{2} - 1} = x^\frac{1}{2} $
*). Menentukan panjang busurnya :
$ \begin{align} \text{Panjang busur } & = \int \limits_a^b \sqrt{ 1 + \left( \frac{dy}{dx} \right)^2 } \, dx \\ & = \int \limits_0^3 \sqrt{ 1 + \left( x^\frac{1}{2} \right)^2 } \, dx \\ & = \int \limits_0^3 \sqrt{ 1 + x } \, dx \\ & = \int \limits_0^3 ( 1 + x )^\frac{1}{2} \, dx \\ & = [ \frac{2}{3} ( 1 + x )^\frac{3}{2} ]_0^3 \\ & = [ \frac{2}{3} ( 1 + 3 )^\frac{3}{2} ] - [ \frac{2}{3} ( 1 + 0 )^\frac{3}{2} ] \\ & = [ \frac{2}{3} . 8 ] - [ \frac{2}{3} . 1 ] \\ & = \frac{2}{3} . 7 \\ & = \frac{14}{3} \end{align} $
Jadi, panjang busurnya adalah $ \frac{14}{3} \, $ satuan panjang.
Penghitungan untuk soal nomor 1 ini berdasarkan batasan sumbu X yaitu dari $ x = 0 \, $ sampai $ x = 3 \, $ . Bagaimana dengan perhitungan berdasarkan sumbu Y dari $ y = 0 \, $ sampai $ y = 2\sqrt{3} \, $ ? Bisa saja kita menghitung menggunakan sumbu Y, hanya saja untuk soal ini agak sulit terutama ketika mengintegralkan fungsi yang terbentuk.
2). Tentukan panjang busur kurva $ y = 3x \, $ dari titik $ A(0,0) \, $ ke titik $ B(2,6) $ ?
Penyelesaian :
*). Cara I : Berdasarkan sumbu X, dari $ x = 0 \, $ sampai $ x = 2 $ ,
*). Menentukan turunannya :
$ y = 3x \rightarrow \frac{dy}{dx} = 3 $
*). Menentukan panjang busurnya :
$ \begin{align} \text{Panjang busur } & = \int \limits_a^b \sqrt{ 1 + \left( \frac{dy}{dx} \right)^2 } \, dx \\ & = \int \limits_0^2 \sqrt{ 1 + \left( 3 \right)^2 } \, dx \\ & = \int \limits_0^2 \sqrt{ 1 + 9 } \, dx \\ & = \int \limits_0^2 \sqrt{ 10 } \, dx \\ & = [ \sqrt{ 10 } x ]_0^2 \\ & = [ \sqrt{ 10 } .2 ] - [ \sqrt{ 10 } . 0 ] \\ & = [ 2\sqrt{ 10 } ] - [ 0 ] \\ & = 2\sqrt{ 10 } \end{align} $
Jadi, panjang busurnya adalah $ 2\sqrt{ 10 } \, $ satuan panjang.
*). Cara II : Berdasarkan sumbu Y, dari $ y = 0 \, $ sampai $ y = 6 $ ,
*). Menentukan turunannya :
$ y = 3x \rightarrow x = \frac{1}{3}y \rightarrow \frac{dx}{dy} = \frac{1}{3} $
*). Menentukan panjang busurnya :
$ \begin{align} \text{Panjang busur } & = \int \limits_c^d \sqrt{ \left( \frac{dx}{dy} \right)^2 + 1 } \, \, dy \\ & = \int \limits_0^6 \sqrt{ \left( \frac{1}{3} \right)^2 + 1 } \, \, dy \\ & = \int \limits_0^6 \sqrt{ \frac{1}{9} + 1 } \, \, dy \\ & = \int \limits_0^6 \sqrt{ \frac{1+9}{9} } \, \, dy \\ & = \int \limits_0^6 \sqrt{ \frac{10}{9} } \, \, dy \\ & = \int \limits_0^6 \frac{1}{3}\sqrt{ 10 } \, \, dy \\ & = [ \frac{1}{3}\sqrt{ 10 }y ]_0^6 \\ & = [ \frac{1}{3}\sqrt{ 10 }. 6 ] - [ \frac{1}{3}\sqrt{ 10 } . 0 ] \\ & = [ 2\sqrt{ 10 } ] - [ 0 ] \\ & = 2\sqrt{ 10 } \end{align} $
Jadi, panjang busurnya adalah $ 2\sqrt{ 10 } \, $ satuan panjang.
Bagaimana cara menghitung panjang busur (berupa lintasan) jika fungsi $ x = f(t) \, $ dan $ y = g(t) \, $ dengan berjalan selama $ a \leq t \leq b $. Hal ini bisa kita hitung dengan memodivikasi rumus umumnya :
Panjang $ \, = \displaystyle \lim_{n \to \infty} \sum_{k=1}^{n} \sqrt{(\Delta x_k )^2 + ( \Delta y_k )^2 } = \int \limits_a^b \sqrt{(d x )^2 + ( dy )^2 } $
menjadi :
$ \begin{align} \text{Panjang busur } & = \int \limits_a^b \sqrt{(d x )^2 + ( dy )^2 } \\ & = \int \limits_a^b \sqrt{(d x )^2 + ( dy )^2 } \times \frac{dt}{dt} \\ & = \int \limits_a^b \frac{ \sqrt{(d x )^2 + ( dy )^2 } } {dt} \, \, dt \\ & = \int \limits_a^b \frac{ \sqrt{(d x )^2 + ( dy )^2 } } {(dt)^2} \, \, dt \\ & = \int \limits_a^b \sqrt{ \frac{ (d x )^2 + ( dy )^2 } {(dt)^2} } \, \, dt \\ & = \int \limits_a^b \sqrt{ \frac{ (d x )^2 } {(dt)^2} + \frac{ ( dy )^2 } {(dt)^2} } \, \, dt \\ & = \int \limits_a^b \sqrt{ \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 } \, \, dt \end{align} $
Rumus Menentukan Panjang Busur yang berkaitan dengan fungsi lain
Cara menghitung panjang busur (berupa lintasan) jika fungsi $ x = f(t) \, $ dan $ y = g(t) \, $ dengan berjalan selama $ a \leq t \leq b $.
Panjang busur $ \, = \int \limits_a^b \sqrt{ \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 } \, \, dt $
Panjang busur $ \, = \int \limits_a^b \sqrt{ \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 } \, \, dt $
3). Misalkan suatu partikel berjalan sepanjang suatu lintasan pada koordinat cartesius yang memenuhi persamaan $ x = 3t \, $ dan $ y = \frac{8}{3} t^\frac{3}{2} $, dengan $ t \, $ dalam menit. Tentukan panjang lintasan yang ditempuh oleh partikel tersebut setelah 1 menit dari titik asal.?
Penyelesaian :
*). Menentukan turunan masing-masing :
$ x = 3t \rightarrow \frac{dx}{dt} = 3 $
$ y = \frac{8}{3} t^\frac{3}{2} \rightarrow \frac{dy}{dt} = \frac{8}{3} . \frac{3}{2}t^\frac{1}{2} = 4t^\frac{1}{2}$
*). Menentukan panjang lintasan partikel :
$ \begin{align} \text{Panjang lintasan } & = \int \limits_a^b \sqrt{ \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 } \, \, dt \\ & = \int \limits_a^b \sqrt{ \left( 3 \right)^2 + \left( 4t^\frac{1}{2} \right)^2 } \, \, dt \\ & = \int \limits_0^1 \sqrt{ 9 + 16t } \, \, dt \\ & = \int \limits_0^1 ( 9 + 16t )^\frac{1}{2} \, \, dt \\ & = [ \frac{1}{16} . \frac{2}{3} ( 9 + 16t )^\frac{3}{2} ]_0^1 \\ & = [ \frac{1}{24} ( 9 + 16t )^\frac{3}{2} ]_0^1 \\ & = [ \frac{1}{24} ( 9 + 16.1 )^\frac{3}{2} ] - [ \frac{1}{24} ( 9 + 16.0 )^\frac{3}{2} ] \\ & = [ \frac{1}{24} ( 25 )^\frac{3}{2} ] - [ \frac{1}{24} ( 9 )^\frac{3}{2} ] \\ & = [ \frac{1}{24} . 125 ] - [ \frac{1}{24} . 27 ] \\ & = \frac{1}{24} ( 125 - 27 ) \\ & = \frac{1}{24} ( 98 ) \\ & = \frac{98}{24} = \frac{49}{12} \\ & = 4\frac{1}{12} \end{align} $
Jadi, panjang lintasan yang ditempuh oleh partikel tersebut selama 1 menit adalah $ 4\frac{1}{12} \, $ satuan panjang.
