Perhatikan daerah yang diarsir berikut ini :
Jika kita diminta untuk menghitung luas daerah yang diarsir di atas, bagaimanakah caranya?
Nah, disinilah ide si jenius Rieman keluar. Caranya, Riemann melakukan pendekatan dengan membagi daerah arsiran tersebut menjadi beberapa persegi panjang, lalu semua luas persegi panjang tersebut dijumlahkan seperti nampak seperti gambar berikut ini.
Persegi panjang 1 memiliki luas $ A_1 \, $ dengan panjang $\Delta x_1 \, $ dan lebar $ f(x_1) $ .
dengan $ A_1 = p \times l = f(x_1) \Delta x_1 $
Persegi panjang 2 memiliki luas $ A_2 \, $ dengan panjang $\Delta x_2 \, $ dan lebar $ f(x_2) $ .
dengan $ A_2 = p \times l = f(x_2) \Delta x_2 $
Persegi panjang 3 memiliki luas $ A_3 \, $ dengan panjang $\Delta x_3 \, $ dan lebar $ f(x_3) $ .
dengan $ A_3 = p \times l = f(x_3) \Delta x_3 $
dan seterusnya ..............
Persegi panjang 8 memiliki luas $ A_8 \, $ dengan panjang $\Delta x_8 \, $ dan lebar $ f(x_8) $ .
dengan $ A_8 = p \times l = f(x_8) \Delta x_8 $
Sehingga luas total persegi panjangnya dinyatakan dalam notasi sigma :
$ \begin{align} A_1 + A_2 + A_3 + ... + A_8 & = f(x_1) \Delta x_1 + f(x_2) \Delta x_2 + f(x_3) \Delta x_3 + ... + f(x_8) \Delta x_8 \\ & = \displaystyle \sum_{i=1}^8 f(x_i) \Delta x_i \end{align} $
Definisi Jumlah Riemann
Nilai dari $ \displaystyle \sum_{i=1}^n f(x_i) \Delta x_i \, $ disebut sebagai Jumlah Riemann fungsi $ f(x) \, $
dengan $ x_i \, $ adalah titik wakil pada interval ke-$i \, $ dan $ \Delta x_i \, $ lebar interval ke-$i \, $ dan $ n \, $ banyak subinterval (banyaknya
persegi panjang yang terbentuk) dari interval $[a,b]$ . Titik wakil $(x_i) \, $ kita peroleh dengan tiga cara yaitu titik ujung kiri subinterval, titik tengah subinterval, dan
titik ujung kanan subinterval, dimana setiap jenis titik wakil memberikan hasil yang berbeda.
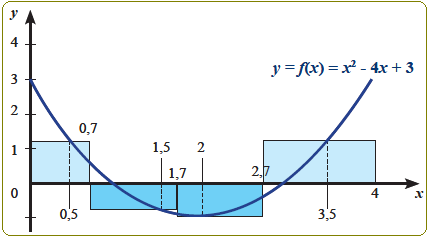
1). Tentukan jumlah Riemann dari fungsi yang diperlihatkan oleh gambar berikut.
*). Menentukan luas persegi panjang masing-masing :
Persegi panjang 1 : panjang = 0,7 , titik wakil $ x_1 = 0,5 \, $
sehingga lebar $ \, = f(x_1) = f(0,5) = (0,5)^2 - 4 (0,5) + 3 = 1,25 $ .
Luas : $ L_1 = p \times l = 0,7 \times 1,25 = 0,875 $
Persegi panjang 2 : panjang = 1,7 - 0,7 = 1 , titik wakil $ x_2 = 1,5 \, $
sehingga lebar $ \, = f(x_2) = f(1,5) = (1,5)^2 - 4 (1,5) + 3 = -0,75 = 0,75 $ .
Luas : $ L_2 = p \times l = 1 \times 0,75 = 0,75 $
Persegi panjang 3 : panjang = 2,7 - 1,7 = 1 , titik wakil $ x_3 = 2 \, $
sehingga lebar $ \, = f(x_3) = f(2) = (2)^2 - 4 (2) + 3 = -1 = 1 $ .
Luas : $ L_3 = p \times l = 1 \times 1 = 1 $
Persegi panjang 4 : panjang = 4 - 2,7 = 1,3 , titik wakil $ x_4 = 3,5 \, $
sehingga lebar $ \, = f(x_4) = f(3,5) = (3,5)^2 - 4 (3,5) + 3 = 1,25 $ .
Luas : $ L_4 = p \times l = 1,3 \times 1,25 = 1,625 $
*). Menentukan jumlah riemannya :
Jumlah riemann $ \, = L_1 + L_2 + L_3 + L_4 = 0,875 + 0,75 + 1 + 1,625 = 4,25 $
Jadi, jumlah riemann pada gambar adalah 4,25.
2). Misalkan diketahui suatu fungsi $ f(x) = x $ pada interval [0, 3], tentukan jumlah Riemann dengan menggunakan 6 subinterval sama panjang dan titik wakilnya :
a). titik ujung kanan subinterval
b). titik tengah subinterval
c). titik ujung kiri subinterval
Penyelesaian :
a). titik ujung kanan subinterval
*). Menentukan panjang setiap subinterval $(\Delta x_i ) $ :
Pada interval [0,3] dibagi menjadi 6 subinterval sama panjang, sehingga :
$ \Delta x_i = \Delta x = \frac{3-0}{6} = \frac{3}{6} = 0,5 $
Untuk dapat menentukan jumlah Riemann fungsi $ f(x) = x $ dengan 6 subinterval pada selang [0,3], perhatikan grafik fungsi $ f(x) = x $ pada interval [0, 3] dan titik ujung kanan subinterval, berikut:
Karena yang diminta adalah titik ujung kanan subinterval, maka nilai $ x_i \, $ yang digunakan adalah sebelah kanan setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0,5 \rightarrow f(x_1) = f(0,5) = 0,5 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 1 \rightarrow f(x_2) = f(1) = 1 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1,5 \rightarrow f(x_3) = f(1,5) = 1,5 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 2 \rightarrow f(x_4) = f(2) = 2 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2,5 \rightarrow f(x_5) = f(2,5) = 2,5 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 3 \rightarrow f(x_6) = f(3) = 3 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0,5 + 1 + 1,5 + 2 + 2,5 + 3 ] \times 0,5 \\ & = [ 10,5 ] \times 0,5 \\ & = 5,25 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 5,25.
b). titik tengah subinterval
Untuk dapat menentukan jumlah Riemann fungsi $ f(x) = x $ dengan 6 subinterval pada selang [0,3], perhatikan grafik fungsi $ f(x) = x $ pada interval [0, 3] dan titik tengah subinterval, berikut:
Karena yang diminta adalah titik tengah subinterval, maka nilai $ x_i \, $ yang digunakan adalah nilai tengah setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0,25 \rightarrow f(x_1) = f(0,25) = 0,25 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 0,75 \rightarrow f(x_2) = f(0,75) = 0,75 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1,25 \rightarrow f(x_3) = f(1,25) = 1,25 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 1,75 \rightarrow f(x_4) = f(1,75) = 1,75 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2,25 \rightarrow f(x_5) = f(2,25) = 2,25 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 2,75 \rightarrow f(x_6) = f(2,75) = 2,75 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0,25 + 0,75 + 1,25 + 1,75 + 2,25 + 2,75 ] \times 0,5 \\ & = [ 9 ] \times 0,5 \\ & = 4,5 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 4,5.
c). titik ujung kiri subinterval
Untuk dapat menentukan jumlah Riemann fungsi $ f(x) = x $ dengan 6 subinterval pada selang [0,3], perhatikan grafik fungsi $ f(x) = x $ pada interval [0, 3] dan titik ujung kiri subinterval, berikut:
Karena yang diminta adalah titik ujung kanan subinterval, maka nilai $ x_i \, $ yang digunakan adalah sebelah kiri setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0 \rightarrow f(x_1) = f(0) = 0 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 0,5 \rightarrow f(x_2) = f(0,5) = 0,5 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1 \rightarrow f(x_3) = f(1) = 1 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 1,5 \rightarrow f(x_4) = f(1,5) = 1,5 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2 \rightarrow f(x_5) = f(2) = 2 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 2,5 \rightarrow f(x_6) = f(2,5) = 2,5 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0 + 0,5 + 1 + 1,5 + 2 + 2,5 ] \times 0,5 \\ & = [ 7,5 ] \times 0,5 \\ & = 3,75 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 3,75.
Catatan :
Sebenarnya untuk menentukan jumlah Riemann, tanpa gambarpun tidak apa-apa.
3). Misalkan diketahui suatu fungsi $ f(x) = x^2 $ pada interval [0, 3], tentukan jumlah Riemann dengan menggunakan 6 subinterval sama panjang dan titik ujung kanan subinterval sebagai titik wakil tiap-tiap subinterval.
Penyelesaian :
*). Menentukan panjang setiap subinterval $(\Delta x_i ) $ :
Pada interval [0,3] dibagi menjadi 6 subinterval sama panjang, sehingga :
$ \Delta x_i = \Delta x = \frac{3-0}{6} = \frac{3}{6} = 0,5 $
*). Menentukan titik wakil $(x_i) $ dengan membagi menjadi 6 subinterval :
Karena yang diminta adalah titik ujung kanan subinterval, maka nilai $ x_i \, $ yang digunakan adalah sebelah kanan setiap subintervalnya.
*). Menentukan lebar (tinggi ) masing-masing subinterval dengan fungsi $ f(x) = x^2 $
Subinterval 1 : 0 - 0,5 dengan $ x_1 = 0,5 \rightarrow f(x_1) = f(0,5) = 0,5^2 = 0,25 $
Subinterval 2 : 0,5 - 1 dengan $ x_2 = 1 \rightarrow f(x_2) = f(1) = 1^2 = 1 $
Subinterval 3 : 1 - 1,5 dengan $ x_3 = 1,5 \rightarrow f(x_3) = f(1,5) = 1,5^2 = 2,25 $
Subinterval 4 : 1,5 - 2 dengan $ x_4 = 2 \rightarrow f(x_4) = f(2) = 2^2 = 4 $
Subinterval 5 : 2 - 2,5 dengan $ x_5 = 2,5 \rightarrow f(x_5) = f(2,5) = 2,5^2 = 6,25 $
Subinterval 6 : 2,5 - 3 dengan $ x_6 = 3 \rightarrow f(x_6) = f(3) = 3^2 = 9 $
*). Menentukan jumlah Riemann :
$ \begin{align} \text{Jumlah Riemann } & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x_i \\ & = \displaystyle \sum_{i=1}^6 f(x_i) \Delta x \\ & = f(x_1) \Delta x + f(x_2) \Delta x + f(x_3) \Delta x + f(x_4) \Delta x + f(x_5) \Delta x + f(x_6) \Delta x \\ & = [ 0,25 + 1 + 2,25 + 4 + 6,25 + 9 ] \times 0,5 \\ & = [ 22,75 ] \times 0,5 \\ & = 11,375 \end{align} $
Jadi, jumlah riemann dengan titik ujung kanan subintervalnya adalah 11,375.
Perhatikan ketiga gambar luasan berikut ini.
Luas Suatu Daerah dengan Jumlah Riemann
Misalkan kita akan menghitung luas suatu daerah yang dibatasi oleh kurva $ y = f(x) \, $ pada selang interval
[a,b] dengan membagi menjadi $ n \, $ subinterval ($n \, $ menuju tak hingga), maka akan kita peroleh luas sebenarnya dengan perhitungan :
Luas $ \, = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $
dengan $ \Delta x_i = \Delta x = \frac{b-a}{n} $ .
penulisan lainnya : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_a^b f(x) dx \, $
Catatan :
Bentuk $ \int \limits_a^b f(x) dx \, $ inilah yang disebut sebagai integral Tentu fungsi $ f(x) \, $ pada interval [a,b] .
Luas $ \, = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $
dengan $ \Delta x_i = \Delta x = \frac{b-a}{n} $ .
penulisan lainnya : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_a^b f(x) dx \, $
Catatan :
Bentuk $ \int \limits_a^b f(x) dx \, $ inilah yang disebut sebagai integral Tentu fungsi $ f(x) \, $ pada interval [a,b] .
Untuk memudahkan dalam pengerjaan jumlah riemann, sebaiknya kita pelajari rumus umum notasi sigma berikut ini :
i). $ \displaystyle \sum_{k=1}^{n} \, k = 1 + 2 + 3 + ... + n = \frac{1}{2}n(n+1) $
ii). $ \displaystyle \sum_{k=1}^{n} \, k^2 = 1^2 + 2^2 + 3^2 + ... + n^2 = \frac{1}{6}n(n+1)(2n+1) $
iii). $ \displaystyle \sum_{k=1}^{n} \, k^3 = 1^3 + 2^3 + 3^3 + ... + n^3 = \left( \frac{1}{2}n(n+1) \right)^2 $
Baca juga penyelesaian limit tak hingga.
Contoh Soal :
4). Misalkan diberikan suatu fungsi $ f(x) = x $, tentukan integral tentu dari $ f(x) = x $ pada interval [0, 3] atau $ \int \limits_0^3 x dx $
Penyelesaian :
*). Interval yang diminta [a,b]=[0,3]
*). Menentukan nilai $ \Delta x_i = \Delta x = \frac{b-a}{n} = \frac{3-0}{n} = \frac{3}{n} $
*). Menentukan bentuk umum dari $ f(x_i) $
$ x_1 = 0 + \Delta x = 0 + \frac{3}{n} = \frac{1 \times 3}{n} $
$ x_2 = 0 + 2\Delta x = 0 + \frac{2 \times 3}{n} = \frac{2 \times 3}{n} $
$ x_3 = 0 + 3\Delta x = 0 + \frac{3 \times 3}{n} = \frac{3 \times 3}{n} $
dan seterusnya ........
$ x_i = 0 + i \Delta x = 0 + \frac{i \times 3}{n} = \frac{i \times 3}{n} $
Untuk bentuk $ f(x) = x \, $ , maka $ f(x_i) = \frac{i \times 3}{n} $
*). Menentukan jumlah riemannya :
$ \begin{align} \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{i \times 3}{n} \frac{3}{n} \\ & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n i \times \frac{9}{n^2} \\ & = \displaystyle \lim_{n \to \infty} \frac{9}{n^2} \sum_{i=1}^n i \, \, \, \, \, \, \text{(gunakan rumus notasi sigma)} \\ & = \displaystyle \lim_{n \to \infty} \frac{9}{n^2} [\frac{1}{2}n(n+1)] \\ & = \displaystyle \lim_{n \to \infty} \frac{\frac{9}{2}n(n+1)}{n^2} \\ & = \displaystyle \lim_{n \to \infty} \frac{\frac{9}{2}n^2 + \frac{9}{2}n }{n^2} \\ & = \frac{9}{2} \end{align} $
Sehingga nilai dari $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_0^3 x dx = \frac{9}{2} $
5). Misalkan diberikan suatu fungsi $ f(x) = x^2 $, tentukan integral tentu dari $ f(x) = x^2 $ pada interval [0, 2] atau $ \int \limits_0^2 x^2 dx $
Penyelesaian :
*). Interval yang diminta [a,b]=[0,2]
*). Menentukan nilai $ \Delta x_i = \Delta x = \frac{b-a}{n} = \frac{2-0}{n} = \frac{2}{n} $
*). Menentukan bentuk umum dari $ f(x_i) $
$ x_1 = 0 + \Delta x = 0 + \frac{2}{n} = \frac{1 \times 2}{n} $
$ x_2 = 0 + 2\Delta x = 0 + \frac{2 \times 2}{n} = \frac{2 \times 2}{n} $
$ x_3 = 0 + 3\Delta x = 0 + \frac{3 \times 2}{n} = \frac{3 \times 2}{n} $
dan seterusnya ........
$ x_i = 0 + i \Delta x = 0 + \frac{i \times 2}{n} = \frac{i \times 2}{n} $
Untuk bentuk $ f(x) = x^2 \, $ , maka $ f(x_i) = \left( \frac{i \times 2}{n} \right)^2 = \frac{4}{n^2} \times i^2 $
*). Menentukan jumlah riemannya :
$ \begin{align} \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{4}{n^2} \times i^2 \frac{2}{n} \\ & = \displaystyle \lim_{n \to \infty} \sum_{i=1}^n i^2 \times \frac{8}{n^3} \\ & = \displaystyle \lim_{n \to \infty} \frac{8}{n^3} \sum_{i=1}^n i^2 \, \, \, \, \, \, \text{(gunakan rumus notasi sigma)} \\ & = \displaystyle \lim_{n \to \infty} \frac{8}{n^3} \frac{1}{6}n(n+1)(2n+1) \\ & = \displaystyle \lim_{n \to \infty} \frac{8}{n^3} \frac{1}{6}(2n^3 + 3n^2 + n) \\ & = \displaystyle \lim_{n \to \infty} \frac{4}{n^3} \frac{1}{3}(2n^3 + 3n^2 + n) \\ & = \displaystyle \lim_{n \to \infty} \frac{8n^3 + 12n^2 + 4n}{3n^3} \\ & = \frac{8 }{3 } \end{align} $
Sehingga nilai dari $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i = \int \limits_0^2 x^2 dx = \frac{8}{3} $
6). Nyatakan limit berikut sebagai suatu integal tentu :
a). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \sqrt{\frac{4i}{n}} \frac{4}{n} $
b). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \left( 1 + \frac{2i}{n} \right) \frac{2}{n} $
c). $ \displaystyle \lim_{n \to \infty} \frac{1}{n} \left( \cos (\frac{\pi}{n}) + \cos (\frac{2\pi}{n}) + \cos (\frac{3\pi}{n}) + ... + \cos (\frac{n\pi}{n}) \right) $
Penyelesaian :
a). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \sqrt{\frac{4i}{n}} \frac{4}{n} $
*). Berdasarkan rumus : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $ maka :
*). $ \Delta x_i = \frac{b-a}{n} = \frac{4}{n} \rightarrow b - a = 4 $
dengan $ a = 0 \, $ maka $ b - a = 4 \rightarrow b - 0 = 4 \rightarrow b = 4 $.
*). Bentuk $ x_i = i \Delta x_i = i \frac{4}{n} = \frac{4i}{n} $
$ f(x_i) = \sqrt{\frac{4i}{n}} = \sqrt{x_i} \, $ artinya $ f(x) = \sqrt{x} $.
*). Bentuk integral tentunya :
$ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \sqrt{\frac{4i}{n}} \frac{4}{n} = \int \limits_a^b f(x) dx = \int \limits_0^4 \sqrt{x} dx $
Jadi, bentuk integral tentunya adalah $ \int \limits_0^4 \sqrt{x} dx $ .
b). $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \left( 1 + \frac{2i}{n} \right) \frac{2}{n} $
Dari soal ini, bentuk $ 1 + \frac{2i}{n} \, $ , artinya $ x_i = a + i \Delta x_i \, $ , sehingga $ a = 1 $
*). Berdasarkan rumus : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $ maka :
*). $ \Delta x_i = \frac{b-a}{n} = \frac{2}{n} \rightarrow b - a = 2 $
dengan $ a = 1 \, $ maka $ b - a = 2 \rightarrow b - 1 = 2 \rightarrow b = 3 $.
*). Bentuk $ x_i = a + i \Delta x_i = 1 + i \frac{2}{n} = 1 + \frac{2i}{n} $
$ f(x_i) = \left( 1 + \frac{2i}{n} \right) = (x_i) \, $ artinya $ f(x) = x $.
*). Bentuk integral tentunya :
$ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \left( 1 + \frac{2i}{n} \right) \frac{2}{n} = \int \limits_a^b f(x) dx = \int \limits_1^3 x dx $
Jadi, bentuk integral tentunya adalah $ \int \limits_1^3 x dx $ .
c). $ \displaystyle \lim_{n \to \infty} \frac{1}{n} \left( \cos (\frac{\pi}{n}) + \cos (\frac{2\pi}{n}) + \cos (\frac{3\pi}{n}) + ... + \cos (\frac{n\pi}{n}) \right) $
*). Kita jadikan bentuk notasi sigma :
$ \displaystyle \frac{1}{n} \left( \cos (\frac{\pi}{n}) + \cos (\frac{2\pi}{n}) + \cos (\frac{3\pi}{n}) + ... + \cos (\frac{n\pi}{n}) \right) = \displaystyle \sum_{i=1}^n \frac{1}{n} \cos \pi (\frac{i}{n}) $
*). Sehingga soal yang akan kita ubah adalah $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{1}{n} \cos \pi (\frac{i}{n}) $
*). Berdasarkan rumus : $ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i \, $ maka :
*). $ \Delta x_i = \frac{b-a}{n} = \frac{1}{n} \rightarrow b - a = 1 $
dengan $ a = 0 \, $ maka $ b - a = 1 \rightarrow b - 0 = 1 \rightarrow b = 1 $.
*). Bentuk $ x_i = i \Delta x_i = i \frac{1}{n} = \frac{i}{n} $
$ f(x_i) = \cos \pi (\frac{i}{n}) = \cos \pi (x_i) \, $ artinya $ f(x) = \cos \pi x $.
*). Bentuk integral tentunya :
$ \displaystyle \lim_{n \to \infty} \sum_{i=1}^n \frac{1}{n} \cos \pi (\frac{i}{n}) = \int \limits_a^b f(x) dx = \int \limits_0^1 \cos \pi x dx $
Jadi, bentuk integral tentunya adalah $ \int \limits_0^1 \, \cos \pi x \, dx $ .
Bagaimana dengan materi Jumlah Riemann yang ada pada artikel ini? Pasti seru dan menyenangkan yah!!!^_^!!! . Untuk penghitungan bentuk integral tentu, kita tidak perlu menggunakan jumlah riemann seperti contoh di atas. Cara pengerjaannya kita menggunakan Teorema Fundamental Kalukulus II, dengan cara ini akan memudahkan kita dalam mengerjakan semua bentuk integral tertentu.
Kita harus bersyukur dengan lahirnya ilmuan Jerma (Riemann) ini, dengan sumbangsih pengetahuannya kita bisa mempelajari dan bisa menghitung luas suatu daerah dengan jumlah Riemann. Meskipun ilmu terus berkembang sedemikian pesat, hasil pemikiran beliau tetap menjadi salah satu acuan bagi kita terutama yang mendalami materi matematika.
