Konsep Peluang Kejadian Bersyarat
Dua kejadian disebut kejadian bersyarat atau kejadian yang saling bergantung apabila
terjadi atau tidak terjadinya kejadian A akan memengaruhi terjadi atau tidak terjadinya kejadian B.
Peluang terjadinya kejadian A dengan syarat kejadian B telah terjadi terlebih dahulu ditulis $ P(A|B) $ :
$ \begin{align} P(A|B) = \frac{P(A \cap B)}{P(B)} , \end{align} \, $ dengan $ \, P(B) \neq 0 $
Peluang terjadinya kejadian B dengan syarat kejadian A telah terjadi terlebih dahulu ditulis $ P(B|A) $ :
$ \begin{align} P(B|A) = \frac{P(A \cap B)}{P(A)} , \end{align} \, $ dengan $ \, P(A) \neq 0 $
dengan $ P(A \cap B) = \, $ peluang irisan A dan B.
Peluang terjadinya kejadian A dengan syarat kejadian B telah terjadi terlebih dahulu ditulis $ P(A|B) $ :
$ \begin{align} P(A|B) = \frac{P(A \cap B)}{P(B)} , \end{align} \, $ dengan $ \, P(B) \neq 0 $
Peluang terjadinya kejadian B dengan syarat kejadian A telah terjadi terlebih dahulu ditulis $ P(B|A) $ :
$ \begin{align} P(B|A) = \frac{P(A \cap B)}{P(A)} , \end{align} \, $ dengan $ \, P(A) \neq 0 $
dengan $ P(A \cap B) = \, $ peluang irisan A dan B.
Contoh Soal Peluang Kejadian Bersyarat :
1). Sebuah dadu dilempar sekali. Tentukan peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima lebih dahulu.
Penyelesaian :
*). Misal A adalah kejadian munculnya angka prima,
Ruang sampel : S = {1,2,3,4,5,6}, sehingga $ n(S) = 6 $
A = {2,3,5}, sehingga $ n(A) = 3 $.
Peluang kejadian A : $ \begin{align} P(A) = \frac{n(A)}{n(S)} = \frac{3}{6} = \frac{1}{2} \end{align} $
*). Misal B adalah kejadian muncul mata dadu ganjil,
B = {1,3,5} , sehingga irisannya : $ A \cap B \, $ = {3,5} , dengan $ n(A \cap B) = 2 $.
Peluang irisannya : $ \begin{align} P(A \cap B) = \frac{n(A \cap B)}{n(S)} = \frac{2}{6} = \frac{1}{3} \end{align} $
*). Menentukan peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima lebih dahulu : $ P(B|A) $
$ \begin{align} P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{\frac{1}{3}}{\frac{1}{2}} = \frac{2}{3} \end{align} $
Jadi, peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima lebih dahulu adalah $ \frac{2}{3} $ .
Catatan :
*). Kejadian A terjadi lebih dahulu, sehingga A = {2,3,5} adalah sebagai ruang sampel dari kejadian B.
*). Kejadian B : B = {3,5} , sehingga peluang kejadian B adalah $ \frac{2}{3} $.
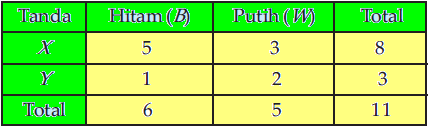
2). Sebuah kotak berisi bola merah dan bola putih, dan setiap bola diberi tanda X atau tanda Y. Berikut komposisi bola-bola yang ada dalam kotak :
Dipilih satu bola secara acak dari kotak tersebut. Tentukan peluang dari kejadian terambil bola hitam bertanda X.
Penyelesaian :
*). Kejadian ini bisa kita pandang sebagai peluang kejadian munculnya bola hitam ( kejadian B) dengan syarat bola bertanda X (kejadian X) lebih dahulu.
*). Terdapat 8 bola bertanda X dari total 11 bola,
sehingga peluangnya $ \, P(X) = \frac{8}{11} $.
*). Dari 8 bola bertanda X terdapat 5 warna hitam, artinya $ n(B \cap X) = 5 $.
sehingga peluangnya $ \, P(B \cap X) = \frac{5}{11} $.
*). Peluang warna hitam (B) dengan syarat bertanda X : $ P(B|X) $
$ \begin{align} P(B|X) = \frac{P(B \cap X)}{P(X)} = \frac{\frac{5}{11}}{\frac{8}{11}} = \frac{5}{8} \end{align} $
Jadi, peluang dari kejadian terambil bola hitam bertanda X adalah $ \frac{5}{8} $.
Menentukan peluang irisan dari peluang kejadian bersyarat
Peluang kejadian A dan B dengan kejadian B terjadi lebih dahulu : $P(A \cap B) $ ,
$ \begin{align} P(A|B) = \frac{P(A \cap B)}{P(B)} \rightarrow P(A \cap B) = P(B) \times P(A|B) \end{align} $
Peluang kejadian A dan B dengan kejadian A terjadi lebih dahulu : $P(A \cap B) $ ,
$ \begin{align} P(B|A) = \frac{P(A \cap B)}{P(A)} \rightarrow P(A \cap B) = P(A) \times P(B|A) \end{align} $
$ \begin{align} P(A|B) = \frac{P(A \cap B)}{P(B)} \rightarrow P(A \cap B) = P(B) \times P(A|B) \end{align} $
Peluang kejadian A dan B dengan kejadian A terjadi lebih dahulu : $P(A \cap B) $ ,
$ \begin{align} P(B|A) = \frac{P(A \cap B)}{P(A)} \rightarrow P(A \cap B) = P(A) \times P(B|A) \end{align} $
Contoh soal :
3). Dalam sebuah kotak terdapat 6 bola merah dan 4 bola putih. Jika sebuah bola diambil dalam kotak itu berturut-turut sebanyak dua kali tanpa pengembalian. Tentukan peluang yang terambil
a). kedua-duanya bola merah,
b). bola pertama warna merah dan bola kedua warna putih.
Penyelesaian :
a). kedua-duanya bola merah,
*). Misal A kejadian bola pertama merah,
Peluang A : $ P(A) = \frac{n(A)}{n(S)} = \frac{6}{10} = \frac{3}{5} $.
*). B kejadian bola kedua warna merah.
karena bola tidak dikembalikan, maka bola merah tinggal 5 bola merah dan 4 bola putih.
Sehingga peluang B dengan kejadian A sudah terjadi : $ P(B|A) $
$ P(B|A) = \frac{5}{9} $
*). Peluang bola pertama merah dan kedua merah : $ P(A \cap B ) $
$ \begin{align} P(A \cap B) = P(A) \times P(B|A) = \frac{3}{5} \times \frac{5}{9} = \frac{1}{3} \end{align} $
Jadi, peluang keduanya merah adalah $ \frac{1}{3} $
b). bola pertama warna merah dan bola kedua warna putih
*). Misal A kejadian bola pertama merah,
Peluang A : $ P(A) = \frac{n(A)}{n(S)} = \frac{6}{10} = \frac{3}{5} $.
*). B kejadian bola kedua warna putih.
karena bola tidak dikembalikan, maka bola merah tinggal 5 bola merah dan 4 bola putih.
Sehingga peluang B dengan kejadian A sudah terjadi : $ P(B|A) $
$ P(B|A) = \frac{4}{9} $
*). Peluang bola pertama merah dan kedua putih : $ P(A \cap B ) $
$ \begin{align} P(A \cap B) = P(A) \times P(B|A) = \frac{3}{5} \times \frac{4}{9} = \frac{4}{15} \end{align} $
Jadi, peluang bola pertama warna merah dan bola kedua warna putih adalah $ \frac{4}{15} $
4). Dalam supermarket terdapat 12 ibu-ibu dan 4 orang remaja yang sedang berbelanja. Kemudian dari mereka dipilih secara acak 3 orang untuk mendapatkan 3 undian berhadiah, dan setiap orang hanya berhak memperoleh 1 hadiah. Tentukan peluang dari kejadian :
a). ketiga undian dimenangkan oleh ibu-ibu.
b). undian pertama dimenangkan remaja, undian kedua dimenangkan oleh ibu-ibu, dan undian ketiga dimenangkan remaja.
c). terdapat 2 undian yang dimenangkan remaja dan 1 undian dimenangkan oleh ibu-ibu.
Penyelesaian :
*). Misalkan I adalah kejadian ibu-ibu memenangkan undian dan R adalah kejadian remaja memenangkan undian.
a). ketiga undian dimenangkan oleh ibu-ibu.
ada 12 ibu-ibuu dan 4 remaja, sehingga $ n(S) = 16 $.
*). Peluang ibu-ibu memenangkan undian pertama : $ P(I_1) = \frac{12}{16} = \frac{3}{4} $.
*). 1 ibu sudah menang, maka tersisa 11 ibu-ibu dan 4 remaja, sehingga
Peluang ibu-ibu memenangkan undian kedua : $ P(I_2|I_1) = \frac{11}{15} $.
*). 2 ibu sudah menang, maka tersisa 10 ibu-ibu dan 4 remaja, sehingga
Peluang ibu-ibu memenangkan undian ketiga : $ P(I_3|I_1,I_2) = \frac{10}{14} = \frac{5}{7} $.
*). Peluang ketiganya dimenangkan oleh ibu-ibu : $ P(I_1 \cap I_2 \cap I_3 ) $
$ \begin{align} P(I_1 \cap I_2 \cap I_3 ) & = P(I_1) \times P(I_2|I_1) \times P(I_3|I_1,I_2) \\ & = \frac{3}{4} \times \frac{11}{15} \times \frac{5}{7} \\ & = \frac{11}{28} \end{align} $
Jadi, peluang ketiga undian dimenangkan oleh ibu-ibu adalah $ \frac{11}{28} $.
b). undian pertama dimenangkan remaja, undian kedua dimenangkan oleh ibu-ibu, dan undian ketiga dimenangkan remaja.
ada 12 ibu-ibuu dan 4 remaja, sehingga $ n(S) = 16 $.
*). Peluang remaja memenangkan undian pertama : $ P(R_1) = \frac{4}{16} = \frac{1}{4} $.
*). 1 remaja sudah menang, maka tersisa 12 ibu-ibu dan 3 remaja, sehingga
Peluang ibu-ibu memenangkan undian kedua : $ P(I|R_1) = \frac{12}{15} = \frac{4}{5} $.
*). 1 ibu sudah menang dan 1 remaja, maka tersisa 11 ibu-ibu dan 3 remaja, sehingga
Peluang remaja memenangkan undian ketiga : $ P(R_2|R_1,I) = \frac{3}{14} $.
*). undian pertama dimenangkan remaja, undian kedua dimenangkan oleh ibu-ibu, dan undian ketiga dimenangkan remaja : $ P(R_1 \cap I \cap R_2 ) $
$ \begin{align} P(R_1 \cap I \cap R_2 ) & = P(R_1) \times P(I|R_1) \times P(R_2|R_1,I) \\ & = \frac{1}{4} \times \frac{4}{5} \times \frac{3}{14} \\ & = \frac{3}{70} \end{align} $
Jadi, peluangnya adalah $ \frac{3}{70} $.
c). terdapat 2 undian yang dimenangkan remaja dan 1 undian dimenangkan oleh ibu-ibu.
Terdapat tiga kemungkinan dan cara menghitungnya mirip dengan cara bagian (b) sebelumnya.
*). undian pertama dimenangkan remaja, undian kedua dimenangkan oleh ibu-ibu, dan undian ketiga dimenangkan remaja,
$ \begin{align} P(R_1 \cap I \cap R_2 ) & = P(R_1) \times P(I|R_1) \times P(R_2|R_1,I) \\ & = \frac{3}{70} = 0,0428 \end{align} $
*). undian pertama dimenangkan remaja, undian kedua dimenangkan oleh remaja, dan undian ketiga dimenangkan ibu-ibu,
$ \begin{align} P(R_1 \cap R_2 \cap I ) & = P(R_1) \times P(R_2|R_1) \times P(I|R_1,R_2) \\ & = \frac{4}{16} \times \frac{3}{15} \times \frac{12}{14} \\ & = 0,0428 \end{align} $
*). undian pertama dimenangkan ibu-ibu, undian kedua dimenangkan oleh remaja, dan undian ketiga dimenangkan remaja,
$ \begin{align} P(I \cap R_1 \cap R_2 ) & = P(I) \times P(R_1|I) \times P(R_2|I,R_1) \\ & = \frac{12}{16} \times \frac{4}{15} \times \frac{3}{14} \\ & = 0,0428 \end{align} $
Jadi, peluang terdapat 2 undian yang dimenangkan remaja dan 1 undian dimenangkan oleh ibu-ibu adalah $ \, 0,0428 + 0,0428 + 0,0428 = 0,1284 $ .