Menentukan Panjang Garis Berat pada Segitiga
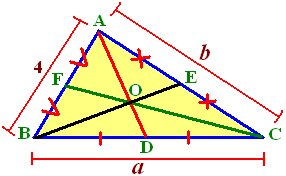
Garis berat sebuah segitiga adalah garis yang melalui sebuah titik sudut dan membagi sisi didepan sudut menjadi dua
bagian sama panjang. Perhatikan gambar garis berat berikut,
Dalil-dalil yang berlaku pada garis berat yaitu :
1). Ketiga garis berat (garis AD, BE, dan CF) berpotongan pada satu titik yang disebut dengan titik berat (titik O).
2). Ketiga garis berat berpotongan pada titik berat dengan bagian-bagiannya memiliki perbandingan 2 : 1, bagian terpanjang adalah titik berat dengan titik sudut ke masing-masing. Perbandingan yang dimaksud adalah AO : OD = 2 : 1, BO : OE = 2 : 1, dan CO : OF = 2 : 1.
3). Panjang garis beratnya bisa kita hitung dengan rumus berikut.
Menentukan panjang garis beratnya.
perhatikan gambar gari berat AD berikut,
Misalkan panjang $ AD = d \, $,
menentukan panjang garis berat dengan rumus :
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 $.
Dalil-dalil yang berlaku pada garis berat yaitu :
1). Ketiga garis berat (garis AD, BE, dan CF) berpotongan pada satu titik yang disebut dengan titik berat (titik O).
2). Ketiga garis berat berpotongan pada titik berat dengan bagian-bagiannya memiliki perbandingan 2 : 1, bagian terpanjang adalah titik berat dengan titik sudut ke masing-masing. Perbandingan yang dimaksud adalah AO : OD = 2 : 1, BO : OE = 2 : 1, dan CO : OF = 2 : 1.
3). Panjang garis beratnya bisa kita hitung dengan rumus berikut.
Menentukan panjang garis beratnya.
perhatikan gambar gari berat AD berikut,
Misalkan panjang $ AD = d \, $,
menentukan panjang garis berat dengan rumus :
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 $.
1). Diketahui segitiga ABC dengan panjang AB = 5 cm, BC = 7 cm , dan AC = 6 cm. Jika garis berat AD dan BE berpotongan di titik O, tentukan panjang AD dan BO!
Penyelesaian :
*). Gambar segitiga ABC dan garis berat AD serta BD.
*). Menentukan panjang garis berat AD.
$ \begin{align} AD^2 & = \frac{1}{2}. AB^2 + \frac{1}{2}.AC^2 - \frac{1}{4}.BC^2 \\ AD^2 & = \frac{1}{2}. 5^2 + \frac{1}{2}.6^2 - \frac{1}{4}.7^2 \\ AD^2 & = \frac{25}{2} + \frac{36}{2} - \frac{49}{4} \\ AD^2 & = \frac{50}{4} + \frac{72}{4} - \frac{49}{4} \\ AD^2 & = \frac{73}{4} \\ AD & = \sqrt{\frac{73}{4}} \\ AD & = \frac{1}{2}\sqrt{73} \end{align} $
Sehingga panjang garis berat $ AD = \frac{1}{2}\sqrt{73} \, $ cm.
*). Menentukan panjang garis berat BE.
$ \begin{align} BE^2 & = \frac{1}{2}. AB^2 + \frac{1}{2}.BC^2 - \frac{1}{4}.AC^2 \\ BE^2 & = \frac{1}{2}. 5^2 + \frac{1}{2}.7^2 - \frac{1}{4}.6^2 \\ BE^2 & = \frac{25}{2} + \frac{49}{2} - \frac{36}{4} \\ BE^2 & = \frac{50}{4} + \frac{98}{4} - \frac{36}{4} \\ BE^2 & = \frac{112}{4} = 28 = 4.7 \\ BE & = \sqrt{4.7} \\ BE & = 2\sqrt{7} \end{align} $
Sehingga panjang garis berat $ BE = 2\sqrt{7} \, $ cm.
*). Berdasarkan perbandingan titik berat, perbandingan BO : OE = 2 : 1,
Sehingga : $ BO = \frac{2}{3}BE = \frac{2}{3}. 2\sqrt{7} = \frac{4}{3}\sqrt{7} $.
Jadi, panjang $ BE = \frac{4}{3}\sqrt{7} \, $ cm.
2). Garis tinggi AD dan garis berat BE berpotongan di titik O pada segitiga ABC dengan panjang sisi-sisinya AB = 4 cm, BC = 6 cm, dan AC = 5 cm. Tentukan panjang OE!.
Penyelesaian :
*). Gambar ilustrasinya.
*). Menentukan panjang garis berat BE.
$ \begin{align} BE^2 & = \frac{1}{2}. AB^2 + \frac{1}{2}.BC^2 - \frac{1}{4}.AC^2 \\ BE^2 & = \frac{1}{2}. 4^2 + \frac{1}{2}.6^2 - \frac{1}{4}.5^2 \\ BE^2 & = \frac{16}{2} + \frac{36}{2} - \frac{25}{4} \\ BE^2 & = \frac{32}{4} + \frac{72}{4} - \frac{25}{4} \\ BE^2 & = \frac{79}{4} \\ BE & = \sqrt{\frac{79}{4}} \\ BE & = \frac{1}{2}\sqrt{79} \end{align} $
Sehingga panjang garis berat $ BE = \frac{1}{2}\sqrt{79} \, $ cm.
*). Menentukan panjang BD dengan dalil proyeksi pada garis tinggi AD.
$ \begin{align} AC^2 & = AB^2 + BC^2 - 2. BC.BD \\ 5^2 & = 4^2 + 6^2 - 2. 6.BD \\ 12BD & = 27 \\ BD & = \frac{27}{12} = \frac{9}{4} \end{align} $.
Panjang $ DC = BC - BD = 6 - \frac{9}{4} = \frac{15}{4} $
Sehingga perbandingan : $ \frac{BD}{DC} = \frac{\frac{9}{4}}{\frac{15}{4}} = \frac{9}{15} = \frac{3}{5} $.
*). Dalil Menelaus untuk EB dengan perbandingan EO : OB.
$ \begin{align} \frac{EO}{OB}. \frac{BD}{DC}. \frac{CA}{EA} & = 1 \\ \frac{EO}{OB}. \frac{3}{5}. \frac{2}{1} & = 1 \\ \frac{EO}{OB}. \frac{6}{5} & = 1 \\ \frac{EO}{OB} & = \frac{5}{6} \end{align} $.
Dari perbandingan EO : OB = 5 : 6, maka
$ OE = \frac{5}{11} BE = \frac{5}{11} . \frac{1}{2}\sqrt{79} = \frac{5}{22} \sqrt{79} $ .
Jadi, panjang $ OE = \frac{5}{22} \sqrt{79} \, $ cm.
3). Terdapat segitiga ABC dengan garis berat AD = $ \sqrt{10}, \, BE = \sqrt{31}, \, $ CF dan panjang AB = 4 cm. Tentukan panjang sisi-sisi segitiga lainnya dan panjang garis berat CF!
Penyelesaian :
*). Ilustrasi gambar segitiga ABC.
*). Menyusun persamaan dari panjang garis berat.
Garis berat $ AD = \sqrt{10} $
$ \begin{align} AD^2 & = \frac{1}{2} AB^2 + \frac{1}{2}AC^2 - \frac{1}{4} BC^2 \\ (\sqrt{10})^2 & = \frac{1}{2} .4^2 + \frac{1}{2} b^2 - \frac{1}{4} a^2 \\ 10 & = 8 + \frac{1}{2} b^2 - \frac{1}{4} a^2 \, \, \, \, \, \text{(kali 4)} \\ 40 & = 32 + 2b^2 - a^2 \\ -a^2 + 2b^2 & = 8 \, \, \, \, \, \text{....pers(i)} \end{align} $
Garis berat $ BE = \sqrt{31} $
$ \begin{align} BE^2 & = \frac{1}{2} AB^2 + \frac{1}{2}BC^2 - \frac{1}{4} AC^2 \\ (\sqrt{31})^2 & = \frac{1}{2} .4^2 + \frac{1}{2} a^2 - \frac{1}{4} b^2 \\ 31 & = 8 + \frac{1}{2} a^2 - \frac{1}{4} b^2 \, \, \, \, \, \text{(kali 4)} \\ 124 & = 32 + 2a^2 - b^2 \\ 2a^2 - b^2 & = 92 \, \, \, \, \, \text{....pers(ii)} \end{align} $
*). eliminasi pers(i) dan pers(ii) :
$ \begin{array}{c|c|cc} -a^2 + 2b^2 = 8 & \text{kali 2} & -2a^2 + 4b^2 = 16 & \\ 2a^2 - b^2 = 92 & \text{kali 2} & 2a^2 - b^2 = 92 & + \\ \hline & & 3b^2 = 108 & \\ & & b^2 = 36 & \\ & & b = 6 & \end{array} $
Pers(i) : $ -a^2 + 2b^2 = 8 \rightarrow -a^2 + 2. 6^2 = 8 \rightarrow a^2 = 64 \rightarrow a = 8 $.
Kita peroleh panjang sisi-sisi segitiganya : AB = 4 cm, BC = 8 cm, dan AC = 6 cm.
*). Menentukan panjang garis berat CF,
$ \begin{align} CF^2 & = \frac{1}{2} BC^2 + \frac{1}{2}AC^2 - \frac{1}{4} AB^2 \\ & = \frac{1}{2} .8^2 + \frac{1}{2}.6^2 - \frac{1}{4} .4^2 \\ & = 32 + 18 - 4 \\ CF^2 & = 46 \\ CF & = \sqrt{46} \end{align} $
Jadi, panjang garis berat $ CF = \sqrt{46} \, $ cm.
4). Segitiga ABC siku-siku di A. Garis berat AD tegak lurus garis berat BE berpotongan di titik O. Jika panjang $ AB = x , \, $ maka tentukan panjang BE!
Penyelesaian :
*). ilustrasi gambar segitiga ABC,
*). Menyusun persamaan dari tegak lurus.
Segitiga ABC siku-siku di A :
$ AB^2 + AC^2 = BC^2 \rightarrow x^2 + b^2 = a^2 \rightarrow b^2 - a^2 = -x^2 \, $ ....pers(i)
Segitiga AOB siku-siku di titik O :
BO : OE = 2 : 1, sehingga $ BO = \frac{2}{3}BE $.
AO : OD = 2 : 1, sehingga $ AO = \frac{2}{3}AD $.
$ AO^2 + OB^2 = AB^2 \rightarrow (\frac{2}{3}AD)^2 + (\frac{2}{3}BE)^2 = x^2 $
$ \frac{4}{9}AD^2 + \frac{4}{9}BE^2 = x^2 \rightarrow AD^2 + BE^2 = \frac{9}{4}x^2 \, $ ....pers(ii).
*). Menyusun persamaan dari garis berat.
Garis berat $ AD $
$ \begin{align} AD^2 & = \frac{1}{2} AB^2 + \frac{1}{2}AC^2 - \frac{1}{4} BC^2 \\ AD^2 & = \frac{1}{2} x^2 + \frac{1}{2}b^2 - \frac{1}{4} a^2 \, \, \, \, \, \text{....pers(iii)} \end{align} $
Garis berat $ BE = \sqrt{31} $
$ \begin{align} BE^2 & = \frac{1}{2} AB^2 + \frac{1}{2}BC^2 - \frac{1}{4} AC^2 \\ BE^2 & = \frac{1}{2} x^2 + \frac{1}{2}a^2 - \frac{1}{4} b^2 \, \, \, \, \, \text{....pers(iv)} \end{align} $
*). Eliminasi pers(iii) dan pes(iv) dan gunakan pers(ii)
$ \begin{array}{cc} AD^2 = \frac{1}{2} x^2 + \frac{1}{2}b^2 - \frac{1}{4} a^2 & \\ BE^2 = \frac{1}{2} x^2 + \frac{1}{2}a^2 - \frac{1}{4} b^2 & - \\ \hline AD^2 - BE^2 = \frac{1}{2}(b^2-a^2) + \frac{1}{4}(b^2 - a^2) & \\ AD^2 - BE^2 = \frac{3}{4}(b^2-a^2) & \\ AD^2 - BE^2 = \frac{3}{4}(-x^2) & \\ AD^2 - BE^2 = -\frac{3}{4}x^2 & \end{array} $
Kita peroleh : $ AD^2 - BE^2 = -\frac{3}{4}x^2 \, $ ....pers(v).
*). Eliminasi pers(ii) dan pers(v) :
$\begin{array}{cc} AD^2 + BE^2 = \frac{9}{4}x^2 & \\ AD^2 - BE^2 = -\frac{3}{4}x^2 & - \\ \hline 2BE^2 = 3x^2 & \\ BE^2 = \frac{3}{2} x^2 & \end{array} $
Dari bentuk $ BE^2 = \frac{3}{2} x^2 $, kita peroleh :
$ BE^2 = \frac{3}{2} x^2 \rightarrow BE^2 = \frac{6}{4} x^2 \rightarrow BE = \sqrt{\frac{6}{4} x^2 } = \frac{1}{2}x\sqrt{6} $.
Jadi, kita peroleh panjang $ BE = \frac{1}{2}x\sqrt{6} $.
Pembuktian perbandingan pada dalil 2 garis berat.
Dalil 2 garis berat berbunyi :
Ketiga garis berat berpotongan pada titik berat dengan bagian-bagiannya memiliki perbandingan 2 : 1, bagian terpanjang adalah titik berat dengan titik sudut ke masing-masing. Perbandingan yang dimaksud adalah AO : OD = 2 : 1, BO : OE = 2 : 1, dan CO : OF = 2 : 1.
Untuk membuktikan dalil ini, kita menggunakan dalil Menenlaus,
Perhatikan gambar berikut.
*). Dalil Menelaus untuk gambar (a).
Perbandingan AO : OD dengan $ \frac{AF}{FB} = 1 \, $ dan $ \frac{BC}{CD} = \frac{2}{1} $
$ \begin{align} \frac{DO}{OA}. \frac{AF}{FB}.\frac{BC}{DC} & = 1 \\ \frac{DO}{OA}. 1.\frac{2}{1} & = 1 \\ \frac{DO}{OA} & = \frac{1}{2} \\ \frac{AO}{OD} & = \frac{2}{1} \end{align} $
Perbandingan CO : OF dengan $ \frac{CD}{DB} = 1 \, $ dan $ \frac{BA}{FA} = \frac{2}{1} $
$ \begin{align} \frac{FO}{OC}. \frac{CD}{DB}.\frac{BA}{FA} & = 1 \\ \frac{FO}{OC}. 1.\frac{2}{1} & = 1 \\ \frac{FO}{OC} & = \frac{1}{2} \\ \frac{CO}{OF} & = \frac{2}{1} \end{align} $
*). Dalil Menelaus untuk gambar (b).
Perbandingan BO : OE dengan $ \frac{BD}{DC} = 1 \, $ dan $ \frac{CA}{EA} = \frac{2}{1} $
$ \begin{align} \frac{EO}{OB}. \frac{BD}{DC}.\frac{CA}{EA} & = 1 \\ \frac{EO}{OB}. 1.\frac{2}{1} & = 1 \\ \frac{EO}{OB} & = \frac{1}{2} \\ \frac{BO}{OE} & = \frac{2}{1} \end{align} $
Jadi, terbukti AO : OD = 2 : 1, BO : OE = 2 : 1, dan CO : OF = 2 : 1.
Ketiga garis berat berpotongan pada titik berat dengan bagian-bagiannya memiliki perbandingan 2 : 1, bagian terpanjang adalah titik berat dengan titik sudut ke masing-masing. Perbandingan yang dimaksud adalah AO : OD = 2 : 1, BO : OE = 2 : 1, dan CO : OF = 2 : 1.
Untuk membuktikan dalil ini, kita menggunakan dalil Menenlaus,
Perhatikan gambar berikut.
*). Dalil Menelaus untuk gambar (a).
Perbandingan AO : OD dengan $ \frac{AF}{FB} = 1 \, $ dan $ \frac{BC}{CD} = \frac{2}{1} $
$ \begin{align} \frac{DO}{OA}. \frac{AF}{FB}.\frac{BC}{DC} & = 1 \\ \frac{DO}{OA}. 1.\frac{2}{1} & = 1 \\ \frac{DO}{OA} & = \frac{1}{2} \\ \frac{AO}{OD} & = \frac{2}{1} \end{align} $
Perbandingan CO : OF dengan $ \frac{CD}{DB} = 1 \, $ dan $ \frac{BA}{FA} = \frac{2}{1} $
$ \begin{align} \frac{FO}{OC}. \frac{CD}{DB}.\frac{BA}{FA} & = 1 \\ \frac{FO}{OC}. 1.\frac{2}{1} & = 1 \\ \frac{FO}{OC} & = \frac{1}{2} \\ \frac{CO}{OF} & = \frac{2}{1} \end{align} $
*). Dalil Menelaus untuk gambar (b).
Perbandingan BO : OE dengan $ \frac{BD}{DC} = 1 \, $ dan $ \frac{CA}{EA} = \frac{2}{1} $
$ \begin{align} \frac{EO}{OB}. \frac{BD}{DC}.\frac{CA}{EA} & = 1 \\ \frac{EO}{OB}. 1.\frac{2}{1} & = 1 \\ \frac{EO}{OB} & = \frac{1}{2} \\ \frac{BO}{OE} & = \frac{2}{1} \end{align} $
Jadi, terbukti AO : OD = 2 : 1, BO : OE = 2 : 1, dan CO : OF = 2 : 1.
Pembuktian Panjang Garis Berat dengan Aturan Cosinus
Untuk materi aturan cosinus, silahkan baca langsung materinya pada artikel
"Penerapan Trigonometri pada Segitiga : Aturan Sinus, Aturan Cosinus, Luas Segitiga".
Perhatikan segitiga ABC berikut.
Panjang $ BD = DC = m = \frac{1}{2}a \, $ dan panjang $ AD = d $.
*). Misalkan sudut $ ABD = y \, $ dan sudut $ ADC = x $.
Sudut $ x \, $ dan $ y \, $ saling berpelurus, sehingga jumlahnya $ 180^\circ$.
$ y + x = 180^\circ \rightarrow y = 180^\circ - x $.
Sehingga : $ \cos y = \cos (180^\circ - x ) = - \cos x $.
*). Aturan Cosinus pada segitiga ABD,
$ c^2 = d^2 + m^2 - 2.d.m .\cos y \rightarrow c^2 = d^2 + m^2 - 2.d.m .(-\cos x) $
$ \rightarrow c^2 = d^2 + m^2 + 2dm\cos x \, $ ....pers(i).
*). Aturan Cosinus pada segitiga ACD,
$ b^2 = d^2 + m^2 - 2.d.m .\cos x \, $ ....pers(ii).
*). Eliminasi pers(i) dan pers(ii) :
$ \begin{array}{cc} c^2 = d^2 + m^2 + 2dm\cos x & \\ b^2 = d^2 + m^2 - 2.d.m .\cos x & + \\ \hline b^2 + c^2 = 2d^2 + 2m^2 & \\ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - m^2 & \\ \end{array} $
Substitusi nilai $ m = \frac{1}{2}a $.
$ \begin{align} d^2 & = \frac{1}{2}b^2 + \frac{1}{2}c^2 - m^2 \\ d^2 & = \frac{1}{2}b^2 + \frac{1}{2}c^2 - (\frac{1}{2}a)^2 \\ d^2 & = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 \end{align} $
Jadi, terbukti panjang garis berat $ \, AD = d \, $ adalah
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 $ .
Perhatikan segitiga ABC berikut.
Panjang $ BD = DC = m = \frac{1}{2}a \, $ dan panjang $ AD = d $.
*). Misalkan sudut $ ABD = y \, $ dan sudut $ ADC = x $.
Sudut $ x \, $ dan $ y \, $ saling berpelurus, sehingga jumlahnya $ 180^\circ$.
$ y + x = 180^\circ \rightarrow y = 180^\circ - x $.
Sehingga : $ \cos y = \cos (180^\circ - x ) = - \cos x $.
*). Aturan Cosinus pada segitiga ABD,
$ c^2 = d^2 + m^2 - 2.d.m .\cos y \rightarrow c^2 = d^2 + m^2 - 2.d.m .(-\cos x) $
$ \rightarrow c^2 = d^2 + m^2 + 2dm\cos x \, $ ....pers(i).
*). Aturan Cosinus pada segitiga ACD,
$ b^2 = d^2 + m^2 - 2.d.m .\cos x \, $ ....pers(ii).
*). Eliminasi pers(i) dan pers(ii) :
$ \begin{array}{cc} c^2 = d^2 + m^2 + 2dm\cos x & \\ b^2 = d^2 + m^2 - 2.d.m .\cos x & + \\ \hline b^2 + c^2 = 2d^2 + 2m^2 & \\ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - m^2 & \\ \end{array} $
Substitusi nilai $ m = \frac{1}{2}a $.
$ \begin{align} d^2 & = \frac{1}{2}b^2 + \frac{1}{2}c^2 - m^2 \\ d^2 & = \frac{1}{2}b^2 + \frac{1}{2}c^2 - (\frac{1}{2}a)^2 \\ d^2 & = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 \end{align} $
Jadi, terbukti panjang garis berat $ \, AD = d \, $ adalah
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 $ .
Pembuktian Panjang Garis Berat dengan Dalil Stewart
Perhatikan segitiga ABC berikut.
Panjang $ BD = DC = m = \frac{1}{2}a \, $ dan panjang $ AD = d $.
*). Dalil Stewart pada segitiga ABC dan substitusi $ m = \frac{1}{2}a $.
$ \begin{align} d^2 . a & = m.b^2 + m.c^2 - m.m.a \\ d^2 . a & = \frac{1}{2}a.b^2 + \frac{1}{2}a.c^2 - \frac{1}{2}a.\frac{1}{2}a.a \, \, \, \, \text{....(bagi } a ) \\ d^2 & = \frac{1}{2} b^2 + \frac{1}{2} c^2 - \frac{1}{4} a^2 \end{align} $
Jadi, terbukti panjang garis berat $ \, AD = d \, $ adalah
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 $ .
Panjang $ BD = DC = m = \frac{1}{2}a \, $ dan panjang $ AD = d $.
*). Dalil Stewart pada segitiga ABC dan substitusi $ m = \frac{1}{2}a $.
$ \begin{align} d^2 . a & = m.b^2 + m.c^2 - m.m.a \\ d^2 . a & = \frac{1}{2}a.b^2 + \frac{1}{2}a.c^2 - \frac{1}{2}a.\frac{1}{2}a.a \, \, \, \, \text{....(bagi } a ) \\ d^2 & = \frac{1}{2} b^2 + \frac{1}{2} c^2 - \frac{1}{4} a^2 \end{align} $
Jadi, terbukti panjang garis berat $ \, AD = d \, $ adalah
$ d^2 = \frac{1}{2}b^2 + \frac{1}{2}c^2 - \frac{1}{4}a^2 $ .