Pengertian Jajajrgenjang
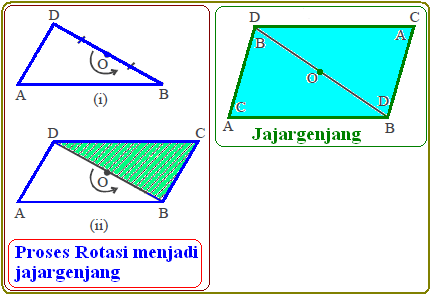
Jajargenjang adalah bangun segi empat yang dibentuk dari
sebuah segitiga dan bayangannya yang diputar setengah putaran ($180^\circ$) pada titik tengah salah satu sisinya.
Keterangan:
*). Segitiga ABD di rotasi (diputar) $180^\circ $ sehingga membentuk jajargenjang ABCD dengan perbaduan segitiga ABD dan segitiga BCD.
*). Segitiga ABD di rotasi (diputar) $180^\circ $ sehingga membentuk jajargenjang ABCD dengan perbaduan segitiga ABD dan segitiga BCD.
Sifat-sifat Jajajrgenjang
Perhatikan jajargenjang ABCD berikut,
Sifat-sifat jajargenjang yaitu :
i). Sisi-sisi yang berhadapan pada setiap jajargenjang sama panjang dan sejajar.
sisi AB = sisi CD dan sejajar, sisi BC = sisi AD dan sejajar.
ii). Sudut-sudut yang berhadapan pada setiap jajargenjang sama besar.
$ \angle ABC = \angle ADC \, $ dan $ \angle BAD = \angle BCD $ .
iii). Jumlah pasangan sudut yang saling berdekatan pada setiap jajargenjang adalah $180^\circ$.
$ \angle BAD + \angle ABC = 180^\circ , \, \angle ABC + \angle BCD = 180^\circ $
$ \angle BCD + \angle ADC = 180^\circ , \, \angle BAD + \angle ADC = 180^\circ $ .
iv). Pada setiap jajargenjang kedua diagonalnya saling membagi dua sama panjang.
Diagonalanya AC dan BD.
panjang AO = OC dan BO = OD.
i). Sisi-sisi yang berhadapan pada setiap jajargenjang sama panjang dan sejajar.
sisi AB = sisi CD dan sejajar, sisi BC = sisi AD dan sejajar.
ii). Sudut-sudut yang berhadapan pada setiap jajargenjang sama besar.
$ \angle ABC = \angle ADC \, $ dan $ \angle BAD = \angle BCD $ .
iii). Jumlah pasangan sudut yang saling berdekatan pada setiap jajargenjang adalah $180^\circ$.
$ \angle BAD + \angle ABC = 180^\circ , \, \angle ABC + \angle BCD = 180^\circ $
$ \angle BCD + \angle ADC = 180^\circ , \, \angle BAD + \angle ADC = 180^\circ $ .
iv). Pada setiap jajargenjang kedua diagonalnya saling membagi dua sama panjang.
Diagonalanya AC dan BD.
panjang AO = OC dan BO = OD.
1). Paerhatikan gambar jajargenjang KLMN berikut,
a. panjang MN;
b. panjang KN;
c. besar $\angle $KNM;
d. besar $\angle $LKN.
Penyelesaian :
a). berdasarkan sifat (i), MN = KL = 10 cm.
b). berdasarkan sifat (i), KN = LM = 8 cm.
c). berdasarkan sifat (ii), $\angle $KNM = $\angle $KLM = 112$^\circ$ .
d). berdasarkan sifat (iii), $ \angle LKN + \angle KLM = 180^\circ $
$ \begin{align} \angle LKN + \angle KLM & = 180^\circ \\ \angle LKN + 112^\circ & = 180^\circ \\ \angle LKN & = 180^\circ - 112^\circ \\ \angle LKN & = 68^\circ \end{align} $
Keliling dan Luas Jajargenjang
Perhatikan jajargenjang ABCD berikut,
$\spadesuit $ Keliling Jajargenjang dari gambar (a),
Keliling jajargenjang (K) : $ K = AB + BC + CD + DA = 2(AB + BC) $.
$\spadesuit $ Luas Jajargenjang
Dari jajargenjang gambar (b), segitiga AED disebelah kiri dipindah kesebelah kanan jajargenjang sehingga terbentuk persegi panjang pada gambar (c). Artinya luas jajargenjang sama dengan luas persegi panjang. Dari gambar (c), panjang AB = $ a \, $ yang merupakan alas jajargenjang dan lebar adalah ED = $ t \, $ yang merupakan tinggi dari jajargenjang.
Luas jajargenjang (L) : $ L = \text{panjang } \times \text{lebar} = a \times t $.
Keliling jajargenjang (K) : $ K = AB + BC + CD + DA = 2(AB + BC) $.
$\spadesuit $ Luas Jajargenjang
Dari jajargenjang gambar (b), segitiga AED disebelah kiri dipindah kesebelah kanan jajargenjang sehingga terbentuk persegi panjang pada gambar (c). Artinya luas jajargenjang sama dengan luas persegi panjang. Dari gambar (c), panjang AB = $ a \, $ yang merupakan alas jajargenjang dan lebar adalah ED = $ t \, $ yang merupakan tinggi dari jajargenjang.
Luas jajargenjang (L) : $ L = \text{panjang } \times \text{lebar} = a \times t $.
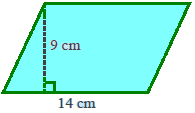
2). Hitunglah luas jajargenjang yang mempunyai alas 14 cm dan tinggi 9 cm.
Penyelesaian :
*). Perhatikan gambar jajargenjang berikut,
$ L = a.t = 14 . 9 = 126 $.
Jadi, luas jajargenjang adalah 126 cm$^2$.
3). Perhatikan gambar jajargenjang KLMN berikut,
b. Hitunglah luas jajargenjang KLMN.
c. Tentukan panjang NP.
Penyelesaian :
a). Menentukan keliling jajargenjang,
Keliling $ = 2(MN + KN ) = 2(28 + 16) = 2 \times 44 = 88 \, $ cm.
b). Luas jajargenjang KLMN,
alasnya kita gunakan LM = KN = 16 , dan tingginya QN = 18 .
Luas = $ a . t = 16 \times 18 = 288 \, $ cm$^2$.
c). Dari bagian (b) di atas, diperoleh luas jajargenjang adalah 288.
untuk menghitung luas jajargenjang juga bisa menggunakan alasnya KL = MN = 28 dan tingginya NP, sehingga
$ \begin{align} \text{Luas jajargenjang } & = a . t \\ 288 & = 28 . NP \\ NP & = \frac{288}{28} = \frac{16 \times 18}{28} = 10\frac{2}{7} \end{align} $
jadi, panjang NP $ = 10\frac{2}{7} \, $ cm.
4). Pada sebuah jajargenjang diketahui luasnya 250 cm$^2$. Jika panjang alas jajargenjang tersebut $ 5x $ dan tingginya $ 2x $, tentukan
a. nilai x;
b. panjang alas dan tinggi jajargenjang tersebut.
Penyelesaian :
a). Menentukan nilai $ x $ ,
$ \begin{align} L & = 250 \\ a . t & = 250 \\ (5x) . (2x) & = 250 \\ 10x^2 & = 250 \\ x^2 & = 25 \\ x & = \sqrt{25} = 5 \end{align} $
sehingga nilai $ x = 5 $ .
b). Panjang alas dan tinggi jajargenjang,
Alas $ = 5x = 5 . 5 = 25 \, $ cm.
Tinggi $ = 2x = 2 . 5 = 10 \, $ cm.
