Menentukan Panjang Garis Tinggi pada Segitiga
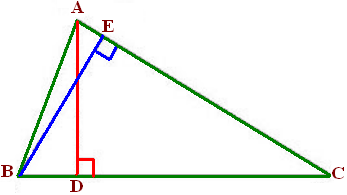
Garis tinggi sebuah segitiga adalah garis yang melalui sebuah titik sudut segitiga dan tegak lurus pada sisi
yang berhadapan dengan titik sudut tersebut. perhatikan gambar garis tinggi berikut,
Dalil-dalil yang berlaku pada garis tinggi segitiga yaitu :
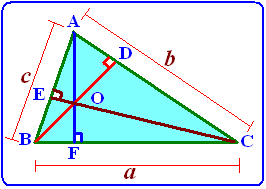
1). Ketiga garis tinggi berpotongan pada satu titik (titik O) yang disebut dengan titik tinggi.
2). Pada segitiga siku-siku, garis tinggi ke hipotenusanya (sisi terpanjang) membagi segitiga siku-siku menjadi dua segitiga yang sebangun dan juga sebangun dengan segitiga awalnya (ketiga segitiga yang ada sebangun) seperti gambar berikut ini,
$\Delta$ABC sebangun dengan $\Delta$ABD sebangun dengan $\Delta$CBD.
3). Menentukan panjang garis tinggi pada segitiga :
Untuk menentukan panjang garis tinggi, kita gunakan Dalil Proyeksi. Ada dua jenis yaitu :
*). Dali proyeksi segitiga lancip,
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.
Misalkan panjang $ CD = p \, $ ,
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 - 2ap $
Misalkan panjang $ BD = k \, $ ,
panjang $ k $ bisa ditentukan dengan rumus: $ \, b^2 = a^2 + c^2 - 2ak $
*). Dali proyeksi segitiga tumpul,
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.

Misalkan panjang $ BD = p \, $ ,
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 + 2ap $
Catatan :
i). Setelah ketemu pajang $ p \, $ , bari kita akan menentukan tinggi segitiganya dengan pythagoras. Artinya kita tidak bisa langsung dapat menentukan tinggi segitiganya, tapi bertahap.
ii). Ada cara lain sehingga tinggi segitiga bisa langsung kita temukan tanpa menjari $ p \, $ terlebih dahulu yaitu menggunakan konsep luas segitiga.
Dalil-dalil yang berlaku pada garis tinggi segitiga yaitu :
1). Ketiga garis tinggi berpotongan pada satu titik (titik O) yang disebut dengan titik tinggi.
2). Pada segitiga siku-siku, garis tinggi ke hipotenusanya (sisi terpanjang) membagi segitiga siku-siku menjadi dua segitiga yang sebangun dan juga sebangun dengan segitiga awalnya (ketiga segitiga yang ada sebangun) seperti gambar berikut ini,
$\Delta$ABC sebangun dengan $\Delta$ABD sebangun dengan $\Delta$CBD.
3). Menentukan panjang garis tinggi pada segitiga :
Untuk menentukan panjang garis tinggi, kita gunakan Dalil Proyeksi. Ada dua jenis yaitu :
*). Dali proyeksi segitiga lancip,
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.
Misalkan panjang $ CD = p \, $ ,
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 - 2ap $
Misalkan panjang $ BD = k \, $ ,
panjang $ k $ bisa ditentukan dengan rumus: $ \, b^2 = a^2 + c^2 - 2ak $
*). Dali proyeksi segitiga tumpul,
Kita proyeksikan garis CA pada garis BC, hasil proyeksinya adalah garis CD seperti gambar berikut.

Misalkan panjang $ BD = p \, $ ,
panjang $ p $ bisa ditentukan dengan rumus: $ \, c^2 = a^2 + b^2 + 2ap $
Catatan :
i). Setelah ketemu pajang $ p \, $ , bari kita akan menentukan tinggi segitiganya dengan pythagoras. Artinya kita tidak bisa langsung dapat menentukan tinggi segitiganya, tapi bertahap.
ii). Ada cara lain sehingga tinggi segitiga bisa langsung kita temukan tanpa menjari $ p \, $ terlebih dahulu yaitu menggunakan konsep luas segitiga.
Menentukan Panjang Garis Tinggi dengan Luas Segitiga
*). Luas segitiga Menggunakan rumus Heron.
Misalkan diketahui sisi-sisi segitiga yaitu $a, \, b, \, $ dan $ \, c $.
$ s = \frac{1}{2}(a+b+c) $
$ \text{Luas } \Delta = \sqrt{s(s-a)(s-b)(s-c)} $.
Untuk pembuktian rumus Heron ini, silahkan baca pada "Penerapan Trigonometri pada Segitiga : Aturan Sinus, Aturan Cosinus, Luas Segitiga".
*). Menentukan panjang garis tinggi,
Perhatikan gambar berikut,
Garis tingginya adalah garis AF, BD, dan CE.
$ \begin{align} AF = t_a & = \frac{2}{a} \sqrt{s(s-a)(s-b)(s-c)} \\ BD = t_b & = \frac{2}{b} \sqrt{s(s-a)(s-b)(s-c)} \\ CE = t_c & = \frac{2}{c} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
Misalkan diketahui sisi-sisi segitiga yaitu $a, \, b, \, $ dan $ \, c $.
$ s = \frac{1}{2}(a+b+c) $
$ \text{Luas } \Delta = \sqrt{s(s-a)(s-b)(s-c)} $.
Untuk pembuktian rumus Heron ini, silahkan baca pada "Penerapan Trigonometri pada Segitiga : Aturan Sinus, Aturan Cosinus, Luas Segitiga".
*). Menentukan panjang garis tinggi,
Perhatikan gambar berikut,
Garis tingginya adalah garis AF, BD, dan CE.
$ \begin{align} AF = t_a & = \frac{2}{a} \sqrt{s(s-a)(s-b)(s-c)} \\ BD = t_b & = \frac{2}{b} \sqrt{s(s-a)(s-b)(s-c)} \\ CE = t_c & = \frac{2}{c} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
1). Sebuah segitiga ABC dengan AB = 5 cm, BC = 6 cm, dan AC = 7 cm. AD adalah garis tinggi segitga ABC, tentukan panjang AD dan luas segitiga ABC.
Penyelesaian :
Cara I : Menggunakan dalil Proyeksi,
*). Menentukan nilai $ p $,
$ \begin{align} c^2 & = a^2 + b^2 - 2ap \\ 5^2 & = 6^2 + 7^2 - 2.6.p \\ 25 & = 36 + 49 - 12p \\ 25 & = 36 + 49 - 12p \\ 12p & = 60 \\ p & = 5 \end{align} $
*). Menentukan panjang AD dengan pythagoras segitiga ADC
$ \begin{align} AC^2 & = AD^2 + DC^2 \\ 7^2 & = AD^2 + 5^2 \\ 49 & = AD^2 + 25 \\ AD^2 & = 24 \\ AD & = \sqrt{24} = 2\sqrt{6} \end{align} $
Sehingga panjang garis tinggi $ AD = 2 \sqrt{6} \, $ cm.
*). Menentukan Luas segitiga ABC.
Luas ABC $ = \frac{1}{2}. a . t = \frac{1}{2}.6 . 2 \sqrt{6} = 6 \sqrt{6} $.
Jadi, luas segitiga ABC adalah $ \, 6 \sqrt{6} \, $ cm$^2$.
Cara II : Menggunakan luas segitiga,
*). Diketahui : $ a = 6, b = 7 , c = 5 $.
$ s = \frac{1}{2}(a+b+c) = \frac{1}{2}(6 + 7 + 5) = \frac{1}{2}.(18) = 9 $.
*). Menentukan panjang AD dengan luas segitiga
$ \begin{align} AD = t_a & = \frac{2}{a} \sqrt{s(s-a)(s-b)(s-c)} \\ & = \frac{2}{6} \sqrt{9(9-6)(9-7)(9-5)} \\ & = \frac{1}{3} \sqrt{9.3.2.4} \\ & = \frac{1}{3} 3.2.\sqrt{6} \\ & = 2\sqrt{6} \end{align} $
Sehingga panjang garis tinggi $ AD = 2 \sqrt{6} \, $ cm.
*). Luas segitiga menggunakan rumus Heron :
$ \begin{align} \text{Luas ABC } & = \sqrt{s(s-a)(s-b)(s-c)} \\ & = \sqrt{9(9-6)(9-7)(9-5)} \\ & = \sqrt{9.3.2.4} \\ & = 3.2.\sqrt{6} \\ & = 6 \sqrt{6} \end{align} $
Jadi, luas segitiga ABC adalah $ \, 6 \sqrt{6} \, $ cm$^2$.
Bagaimana dengan kedua cara di atas, lebih mudah mana, cara I atau cara II. Cara II (rumus Heron) akan mudah kalau panjang semua sisi segitiganya berupa bilangan bulat, dan akan sulit jika salah satu panjang sisi segitiganya dalam bentuk akar. Ini artinya mudah atau tidaknya bersifat relatif.
2). Diketahui persegi panjang ABCD dengan AB = 8 cm dan BC = 6 cm. Titik M dan N terletak pada AC sedemikian sehingga DM dan BN tegak lurus pada AC. Tentukan panjang MN?
Penyelesaian :
*). Gambar persegi panjangnya.
Segitiga ADC siku-siku di D sehingga dengan pythagoras kita peroleh AC = 10 cm.
Garis DM adalah garis tinggi pada segitiga ADC sehingga bisa kita terapkan dalil proyeksi.
*). Menentukan panjang AM pada gambar (b)
$ \begin{align} CD^2 & = AD^2 + AC^2 - 2.AC . AM \\ 8^2 & = 6^2 + 10^2 - 2. 10 . AM \\ 64 & = 36 + 100 - 20. AM \\ AM & = 3,6 \end{align} $
Karena panjang AM = CN, sehingga CN = 3,6 juga.
*). Menentukan panjang MN :
$ \begin{align} MN & = AC - (AM + CN) \\ & = 10 - (3,6 + 3,6) \\ & = 10 - 7,2 \\ & = 2,8 \end{align} $
Jadi, panjang AM = 2,8 cm.
3). Perhatikan gambar segitiga ABC berikut ini,
Diketahui panjang BC = 12 cm, AD = 30 cm , AC = 15 cm. Tentukan panjang garis tinggi BE.
Penyelesaian :
*). Kita gunakan luas segitiga : Luas $ = \frac{1}{2}.a.t$.
$ \begin{align} \text{Luas segitiga ABC dengan alas AC} & = \text{Luas segitiga ABC dengan alas BC} \\ \frac{1}{2}. AC . BE & = \frac{1}{2}.BC . AD \\ AC . BE & = BC . AD \\ 15 . BE & = 12 \times 30 \\ BE & = \frac{12 \times 30}{15} \\ BE & = 24 \end{align} $
Jadi, panjang garis tinggi BE = 24 cm.
4). Sebuah segitiga ABC dengan AB = 5 cm, BC = 7 cm, dan AC = 6 cm. Garis tinggi AD dan BE berpotongan di titik O. Tentukan perbandingan panjang AO:OD dan perbandingan BO : OE.
Penyelesaian :
*). Untuk menjawab soal ini, kita menggunakan garis tinggi (dalil proyeksi) dan dalil Menelaus.
*). Dalil proyeksi untuk garis tinggi AD dan BE.
garis tinggi AD :
$ \begin{align} AC^2 & = AB^2 + BC^2 - 2 . BC . BD \\ 6^2 & = 5^2 + 7^2 - 2 . 7 . BD \\ 36 & = 25 + 49 - 14. BD \\ 36 & = 25 + 49 - 14. BD \\ 14BD & = 38 \\ BD & = \frac{38}{14} = \frac{19}{7} \end{align} $
Sehingga panjang $ DC = 7 - BD = 7 - \frac{19}{7} = \frac{30}{7} $.
garis tinggi BE :
$ \begin{align} BC^2 & = AB^2 + AC^2 - 2 . AC . AE \\ 7^2 & = 5^2 + 6^2 - 2 . 6 . AE \\ 49 & = 25 + 36 - 12. AE \\ AE & = 1 \end{align} $
Sehingga panjang $ CE = 6 - AE = 6 - 1 = 5 $.
*). Dalil Menelaus untuk perbandingan garis,
Perbandingan AO : OD,
$ \begin{align} \frac{DO}{AO}. \frac{AE}{EC}. \frac{CB}{DB} & = 1 \\ \frac{DO}{AO}. \frac{1}{5}. \frac{7}{\frac{19}{7}} & = 1 \\ \frac{DO}{AO}. \frac{1}{5}. \frac{49}{19} & = 1 \\ \frac{DO}{AO}. \frac{49}{95} & = 1 \\ \frac{DO}{AO} & = \frac{95}{49} \end{align} $
Sehingga perbandingan AO : DO = 49 : 95.
Perbandingan BO : OE,
$ \begin{align} \frac{EO}{OB}. \frac{BD}{DC}. \frac{CA}{AE} & = 1 \\ \frac{EO}{OB}. \frac{\frac{19}{7}}{\frac{30}{7}}. \frac{6}{1} & = 1 \\ \frac{EO}{OB}. \frac{19}{30}. \frac{6}{1} & = 1 \\ \frac{EO}{OB}. \frac{19}{5} & = 1 \\ \frac{EO}{OB} & = \frac{5}{19} \end{align} $
Sehingga perbandingan BO : OE = 19 : 5.
Pembuktian dalil Proyeksi
Untuk membuktikan dalil proyeksi, kita cukup menggunakan teorema pythagoras. Perhatikan gambar berikut,
*). Dalil proyeksi segitiga lancip.
Misalkan panjang $ CD = p , \, $ maka panjang $ BD = a - p $.
*). Pada $\Delta$BAD dan $\Delta$CAD masing-masing siku-siku di D sehingga bisa diterapkan pythagoras:
Segitiga CAD : $ AD^2 = b^2 - p^2 \, $ ....pers(i).
Segitiga BAD : $ AD^2 = c^2 - (a-p)^2 \, $ ....pers(ii).
Dari pers(i) dan pers(ii), panjang AD sama, sehingga :
$ \begin{align} c^2 - (a-p)^2 & = b^2 - p^2 \\ c^2 - (a^2 - 2ap + p^2) & = b^2 - p^2 \\ c^2 - a^2 + 2ap - p^2 & = b^2 - p^2 \\ c^2 & = a^2 + b^2 - 2ap \end{align} $
Jadi terbukti persamaan : $ c^2 = a^2 + b^2 - 2ap $.
*). Dalil proyeksi segitiga tumpul.
Misalkan panjang $ BD = p , \, $ maka panjang $ CD = a + p $.
*). Pada $\Delta$ADB dan $\Delta$ADC masing-masing siku-siku di D sehingga bisa diterapkan pythagoras:
Segitiga ADB : $ AD^2 = c^2 - p^2 \, $ ....pers(i).
Segitiga ADC : $ AD^2 = b^2 - (a+p)^2 \, $ ....pers(ii).
Dari pers(i) dan pers(ii), panjang AD sama, sehingga :
$ \begin{align} b^2 - (a+p)^2 & = c^2 - p^2 \\ b^2 - (a^2 + 2ap + p^2) & = c^2 - p^2 \\ b^2 - a^2 - 2ap - p^2 & = c^2 - p^2 \\ b^2 & = a^2 + c^2 + 2ap \end{align} $
Jadi terbukti persamaan : $ b^2 = a^2 + c^2 + 2ap $.
*). Dalil proyeksi segitiga lancip.
Misalkan panjang $ CD = p , \, $ maka panjang $ BD = a - p $.
*). Pada $\Delta$BAD dan $\Delta$CAD masing-masing siku-siku di D sehingga bisa diterapkan pythagoras:
Segitiga CAD : $ AD^2 = b^2 - p^2 \, $ ....pers(i).
Segitiga BAD : $ AD^2 = c^2 - (a-p)^2 \, $ ....pers(ii).
Dari pers(i) dan pers(ii), panjang AD sama, sehingga :
$ \begin{align} c^2 - (a-p)^2 & = b^2 - p^2 \\ c^2 - (a^2 - 2ap + p^2) & = b^2 - p^2 \\ c^2 - a^2 + 2ap - p^2 & = b^2 - p^2 \\ c^2 & = a^2 + b^2 - 2ap \end{align} $
Jadi terbukti persamaan : $ c^2 = a^2 + b^2 - 2ap $.
*). Dalil proyeksi segitiga tumpul.
Misalkan panjang $ BD = p , \, $ maka panjang $ CD = a + p $.
*). Pada $\Delta$ADB dan $\Delta$ADC masing-masing siku-siku di D sehingga bisa diterapkan pythagoras:
Segitiga ADB : $ AD^2 = c^2 - p^2 \, $ ....pers(i).
Segitiga ADC : $ AD^2 = b^2 - (a+p)^2 \, $ ....pers(ii).
Dari pers(i) dan pers(ii), panjang AD sama, sehingga :
$ \begin{align} b^2 - (a+p)^2 & = c^2 - p^2 \\ b^2 - (a^2 + 2ap + p^2) & = c^2 - p^2 \\ b^2 - a^2 - 2ap - p^2 & = c^2 - p^2 \\ b^2 & = a^2 + c^2 + 2ap \end{align} $
Jadi terbukti persamaan : $ b^2 = a^2 + c^2 + 2ap $.
Pembuktian panjang garis tinggi dengan luas segitiga
Berdasarkan rumus luas segitiga dengan rumus Heron,
$ \text{Luas ABC} = \sqrt{s(s-a)(s-b)(s-c)} $ .
Perhatikan gambar segitiga berikut.
*). Perhatikan segitiga ABC dengan alas $ BC = a \, $ dan tinggi $ AF = t_a $
$ \begin{align} \text{Luas ABC} & = \frac{1}{2}. \text{alas}. \text{tinggi} \\ \sqrt{s(s-a)(s-b)(s-c)} & = \frac{1}{2}. a . t_a \\ t_a & = \frac{2}{a} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
*). Perhatikan segitiga ABC dengan alas $ AC = b \, $ dan tinggi $ BD = t_b $
$ \begin{align} \text{Luas ABC} & = \frac{1}{2}. \text{alas}. \text{tinggi} \\ \sqrt{s(s-a)(s-b)(s-c)} & = \frac{1}{2}. b . t_b \\ t_b & = \frac{2}{b} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
*). Perhatikan segitiga ABC dengan alas $ AB = c \, $ dan tinggi $ CE = t_c $
$ \begin{align} \text{Luas ABC} & = \frac{1}{2}. \text{alas}. \text{tinggi} \\ \sqrt{s(s-a)(s-b)(s-c)} & = \frac{1}{2}. c . t_c \\ t_c & = \frac{2}{c} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
Jadi, sudah terbukti panjang garis tinggi yang diminta.
$ \text{Luas ABC} = \sqrt{s(s-a)(s-b)(s-c)} $ .
Perhatikan gambar segitiga berikut.
*). Perhatikan segitiga ABC dengan alas $ BC = a \, $ dan tinggi $ AF = t_a $
$ \begin{align} \text{Luas ABC} & = \frac{1}{2}. \text{alas}. \text{tinggi} \\ \sqrt{s(s-a)(s-b)(s-c)} & = \frac{1}{2}. a . t_a \\ t_a & = \frac{2}{a} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
*). Perhatikan segitiga ABC dengan alas $ AC = b \, $ dan tinggi $ BD = t_b $
$ \begin{align} \text{Luas ABC} & = \frac{1}{2}. \text{alas}. \text{tinggi} \\ \sqrt{s(s-a)(s-b)(s-c)} & = \frac{1}{2}. b . t_b \\ t_b & = \frac{2}{b} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
*). Perhatikan segitiga ABC dengan alas $ AB = c \, $ dan tinggi $ CE = t_c $
$ \begin{align} \text{Luas ABC} & = \frac{1}{2}. \text{alas}. \text{tinggi} \\ \sqrt{s(s-a)(s-b)(s-c)} & = \frac{1}{2}. c . t_c \\ t_c & = \frac{2}{c} \sqrt{s(s-a)(s-b)(s-c)} \end{align} $
Jadi, sudah terbukti panjang garis tinggi yang diminta.