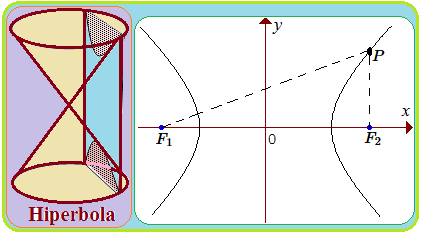
Persamaan Hiperbola dan Unsur-unsurnya
Blog Koma - Materi irisan kerucut mencakup lingkaran, parabola, elips, dan hiperbola, dimana yang sudah kita bahas adalah " persamaan parabol…
Read more »
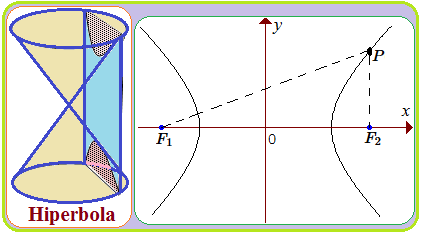
Cara Menemukan Persamaan Hiperbola
Blog Koma - Sebelumnya kita telah belajar tentang " parabola " dan " elips " yang merupakan bagian dari " irisan kerucut …
Read more »
Garis Singgung Elips Titik Diluar Kurva
Blog Koma - Sebelumnya kita telah mempelajari materi " persamaan garis singgung elips " yang mana jenis-jenis persamaan garis singgungny…
Read more »
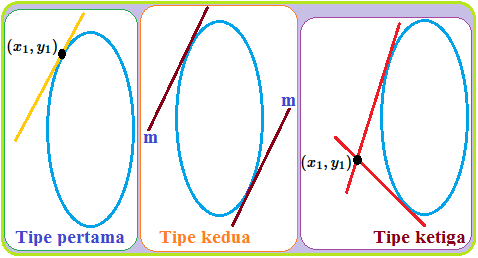
Persamaan Garis Singgung ELips
Blog Koma - Setelah mempelajari materi "kedudukan titik terhadap elips" dan " kedudukan garis terhadap elips " dimana kedua mat…
Read more »
Kedudukan Garis terhadap Elips
Blog Koma - Selain materi " kedudukan titik terhadap elips " yang berkaitan langsung dengan "persamaan elips" yaitu " per…
Read more »
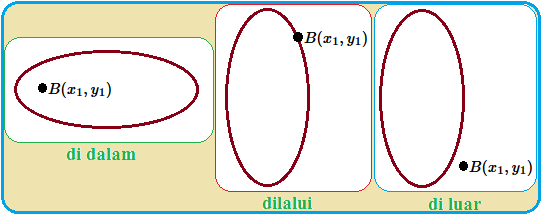
Kedudukan Titik terhadap Elips
Blog Koma - Materi Kedudukan Titik terhadap Elips sangat penting kita bahas karena berkaitan langsung dengan " persamaan garis singgung elip…
Read more »