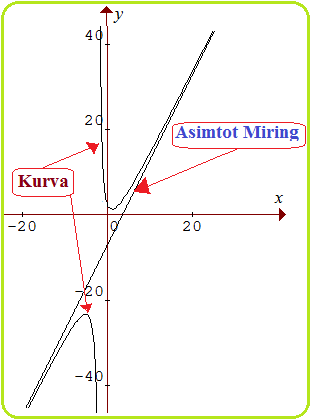
Asimtot Miring Fungsi Aljabar
Blog Koma - Setelah memebahas " asimtot tegak dan mendatar fungsi aljabar ", nah pada artikel ini kita lanjutkan dengan pembahasan mater…
Read more »
Asimtot Tegak dan Mendatar Fungsi Aljabar
Blog Koma - Pada artikel ini kita akan membahas materi Asimtot Tegak dan Mendatar Fungsi Aljabar . Apa sih asimtot itu? Asimtot adalah suatu gari…
Read more »
Limit Tak Hingga Fungsi Trigonometri
Blog Koma - Pada artikel ini kita akan membahas materi Limit Tak Hingga Fungsi Trigonometri . Materi Limit Tak Hingga Fungsi Trigonometri merupakan…
Read more »
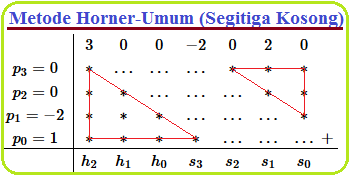
Pembagian Suku Banyak Metode Horner
Sebelumnya kita telah membahas materi " Operasi Pembagian Suku Banyak " dengan penekanan dua cara yaitu cara bersusun dan cara skema horn…
Read more »
Luas dan Keliling Bangun Datar Segi-n Beraturan
Blog Koma - Setelah sebelumnya kita membahas materi " Luas Bangun Datar Diketahui Koordinatnya ", pada artikel ini kita lanjutkan dengan…
Read more »
Luas Bangun Datar Diketahui Koordinatnya
Blog Koma - Pada artikel ini kita akan membahas materi Luasan suatu bangun datar dengan judul Luas Bangun Datar Diketahui Koordinatnya . Luas bang…
Read more »
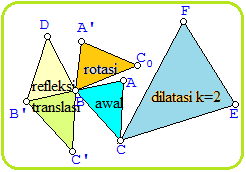
Transformasi Geometri Luas Bangun datar
Blog Koma - Hallow teman-teman, bagaimana kabarnya? Mudah-mudahan baik-baik saja. Pada artikel ini kita akan kembali membahas artikel yang terkait…
Read more »