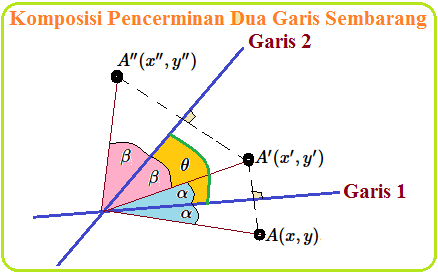
Komposisi Pencerminan Dua Garis Sembarang
Blog Koma - Sebelumnya kita telah mempelajari materi " Komposisi Pencerminan Garis Vertikal atau Horizontal ", pada artikel ini kita lanj…
Read more »
Komposisi Pencerminan Garis Vertikal atau Horizontal
Blog Koma - Pada artikel ini kita akan membahas materi Komposisi Pencerminan Garis Vertikal atau Horizontal . Sebelumnya telah kita bahas materi &…
Read more »
Komposisi Transformasi pada Translasi
Blog Koma - Pada artikel ini kita akan membahas materi Komposisi Transformasi pada Translasi . Artikel ini merupakan kelanjutan dari materi kompos…
Read more »
Komposisi Transformasi dengan Matriks
Blog Koma - Setelah sebelumnya kita membahas materi " Pengertian Komposisi Transformasi Geometri ", pada artikel ini kita lanjutkan deng…
Read more »
Pengertian Komposisi Transformasi Geometri
Blog Koma - Pada artikel sebelumnya kita telah membahas artikel transformasi geometri yang terdiri dari beberapa jenis yaitu translasi, dilatasi,…
Read more »
Penerapan Rumus Trigonometri pada Soal-soal Bagian 1
Blog Koma - Setelah mempelajari materi " rumus jumlah dan selisih sudut pada trigonometri " dan materi "rumus hasil kali antara dua…
Read more »