Refleksi atau Pencerminan pada Transformasi
Blog Koma - Pada artikel ini kita akan membahas materi Refleksi atau Pencerminan pada Transformasi . Tentu teman-teman tidak asing dengan kata pen…
Read more »
Rotasi pada Transformasi Geometri
Blog Koma - Dua jenis transformasi geometri telah kita bahas pada artikel sebelumnya yaitu " translasi " dan " dilatasi ". Pa…
Read more »
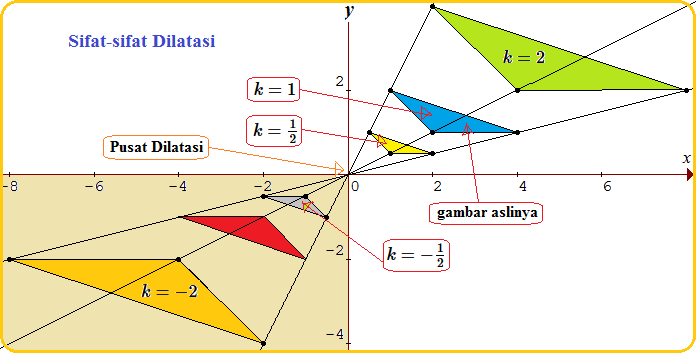
Dilatasi pada Transformasi Geometri
Blog Koma - Setelah mempelajari materi " translasi pada transformasi geometri ", pada artikel ini kita lanjutkan dengan pembahasan salah…
Read more »
Translasi pada Transformasi Geometri
Blog Koma - Setelah membahas materi " Matriks Transformasi Geometri " pada artikel sebelumnya, kita lanjutkan dengan pembahasan jenis-je…
Read more »
Matriks Transformasi Geometri
Blog Koma - Sebenarnya materi transformasi geometri itu apakah sulit bagi teman-teman? Tentu ada sebagian siswa/siswi akan menjawab ya, dan sebag…
Read more »