Berkas Lingkaran
Blog Koma - Kali ini kita akan mempelajari materi berkas lingkaran . Sebelum mempelajarinya, sebaiknya baca dulu materi yang terkait yaitu &quo…
Read more »
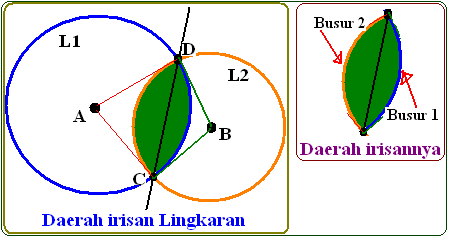
Keliling dan Luas Irisan Dua Lingkaran
Blog Koma - " Irisan dua lingkaran " akan membentuk suatu daerah irisan. Daerah irisan akan terbentuk jika kedua lingkaran berpotonga…
Read more »
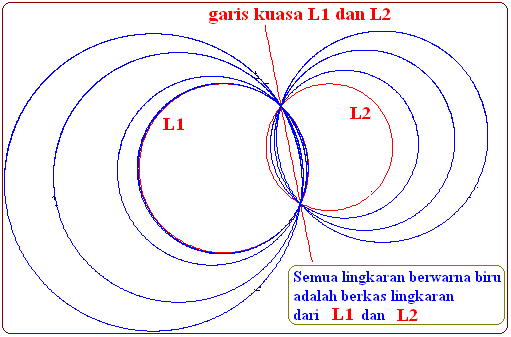
Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaran
Blog Koma - Kali ini kita akan mempelajari materi Kuasa Lingkaran , Titik Kuasa, dan Garis Kuasa Lingkaran . Untuk memudahkan dalam mempe…
Read more »
Garis Singgung Persekutuan Lingkaran
Blog Koma - Garis singgung persekutuan lingkaran maksudnya ada suatu garis yang menyinggung suatu lingkaran baik satu lingkaran , dua lingk…
Read more »
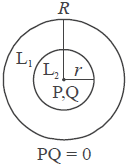
Kedudukan Dua Lingkaran
Blog Koma - Kedudukan Dua Lingkaran maksudnya posisi kedua lingkaran yang dibagi menjadi beberapa jenis. Untuk memudahkan mempelajari materi k…
Read more »
Irisan Dua Lingkaran
Blog Koma - Irisan Dua Lingkaran merupakan materi matematika peminatan. Materi yang akan dipelajari pada irisan dua lingkaran yaitu " ke…
Read more »
Pembuktian Rumus Persamaan Garis Singgung Lingkaran
Blog Koma - Pembuktian Rumus Pesamaan Garis Singgung Lingkaran merupakan penjelasan mengenai asal-usul rumus persamaan garis singgung. Nam…
Read more »
Persamaan Garis Singgung Lingkaran
Blog Koma - Persamaan garis singgung lingkaran merupakan suatu garis yang menyinggung suatu lingkaran. Untuk memudahkan dalam mempelajari per…
Read more »